题目内容
11.已知命题p:对任意x∈R,ax2+2x+a≥0,命题q:存在$x∈R,a({sinx+2{{cos}^2}\frac{x}{2}-1})=\sqrt{2}$,证明p是q的充分不必要条件.分析 分别求出p,q的a的范围,结合集合的包含关系,从而证出结论.
解答 证明:关于命题p:对任意x∈R,ax2+2x+a≥0,
∴$\left\{\begin{array}{l}{a>0}\\{△=4-{4a}^{2}≤0}\end{array}\right.$,解得:a≥1,
∴p为真时:a∈A=[1,+∞);
命题q:存在$x∈R,a({sinx+2{{cos}^2}\frac{x}{2}-1})=\sqrt{2}$,
∴a(sinx+1+cosx-1)=$\sqrt{2}$,
∴asin(x+$\frac{π}{4}$)=1,
∴q真时a∈B=(-∞,-1]∪[1,+∞),
因为A是B的真子集,
∴p是q的充分不必要条件.
点评 本题考查了充分必要条件,考查二次函数、三角函数问题,是一道基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
3.已知函数f(x)=$\frac{2x+3}{3x}$,数列{an}满足a1=1,an+1=f($\frac{1}{{a}_{n}}$),n∈N*.数列{an}的通项公式;( )
| A. | an=$\frac{2}{3}$n+$\frac{1}{3}$ | B. | an=$\frac{2}{3}$n-$\frac{1}{3}$ | C. | an=$\frac{1}{3}$n+$\frac{1}{3}$ | D. | an=$\frac{2}{3}$n+$\frac{1}{4}$ |
6.若a为实数,且2+ai=(1+i)(3+i),则a=( )
| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
16.算法如果执行下面的程序框图,输入n=6,m=4,那么输出的p于( )
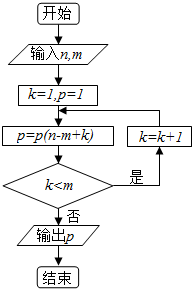

| A. | 12 | B. | 60 | C. | 360 | D. | 48 |
3.满足{-1,0}∪A={-1,0,1}的集合A共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.若全集U=R,A=[1,3],B={x|x2-2x≤0},则A∩(∁UB)=( )
| A. | [1,2] | B. | (-∞,0)∪(2,3] | C. | [0,1) | D. | (2,3] |
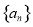 的前
的前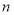 项和为
项和为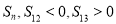 ,则
,则 的最小值为( )
的最小值为( )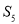 B.
B. C.
C.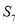 D.
D.