题目内容
15.已知a∈R,集合[a,a2+2]有且只有3个整数,则a的取值范围是{a|$-1<a<\frac{1-\sqrt{5}}{2}$或$\frac{1+\sqrt{5}}{2}<a<2$}.分析 利用已知条件列出不等式组,求解即可得到a的范围.
解答 解:a∈R,集合[a,a2+2]有且只有3个整数,
可得:$\left\{\begin{array}{l}3<{a}^{2}-a+2\\{a}^{2}-a+2<4\end{array}\right.$,解得:$-1<a<\frac{1-\sqrt{5}}{2}$或$\frac{1+\sqrt{5}}{2}<a<2$.
a的取值范围是:{a|$-1<a<\frac{1-\sqrt{5}}{2}$或$\frac{1+\sqrt{5}}{2}<a<2$}
点评 本题考查不等式组的解法,考查转化是的应用.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
5.在△ABC中,若$\overrightarrow{AB}$2>$\overrightarrow{AB}•\overrightarrow{AC}$+$\overrightarrow{BA}•\overrightarrow{BC}$+$\overrightarrow{CA}•\overrightarrow{CB}$,则△ABC是( )
| A. | 不等边三角形 | B. | 三条边不全相等的三角形 | ||
| C. | 锐角三角形 | D. | 钝角三角形 |
6.已知曲线P:y=e3x,曲线Q:y=lnx${\;}^{\frac{1}{3}}$,则曲线P与曲线Q( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于y=x对称 |
4.为了考察两个变量x和y之间的线性相关性,甲、乙两个同学各自独立地作10次和15次试验,并且利用线性回归方法,求得回归直线分别为l1和l2.已知在两个人的试验中发现对变量x的观测数据的平均值恰好相等,都为s,对变量y的观测数据的平均值也恰好相等,都为t.那么下列说法正确的是( )
| A. | 直线l1和l2相交,但是交点未必是点(s,t) | |
| B. | 直线l1和l2有交点(s,t) | |
| C. | 直线l1和l2由于斜率相等,所以必定平行 | |
| D. | 直线l1和l2必定重合 |
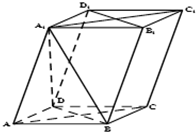 如图,平行六面体体ABCD-A1B1C1D1中,所有棱长均为1,且∠BAD=∠A1AB=∠A1AC=60°.
如图,平行六面体体ABCD-A1B1C1D1中,所有棱长均为1,且∠BAD=∠A1AB=∠A1AC=60°.