题目内容
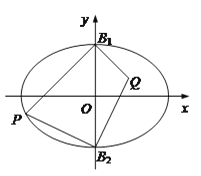
【题目】如图,在平面直角坐标系xOy中,B1,B2是椭圆![]() 的短轴端点,P是椭圆上异于点B1,B2的一动点.当直线PB1的方程为
的短轴端点,P是椭圆上异于点B1,B2的一动点.当直线PB1的方程为![]() 时,线段PB1的长为
时,线段PB1的长为![]() .
.
(1)求椭圆的标准方程;
(2)设点Q满足: ![]()
![]() .求证:△PB1B2与△QB1B2的面积之比为定值.
.求证:△PB1B2与△QB1B2的面积之比为定值.
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:设![]() ,
, ![]() ,(1)根据直线
,(1)根据直线![]() 的方程为
的方程为![]() 时,线段
时,线段![]() 的长为
的长为![]() ,可分别求得
,可分别求得![]() 和
和![]() ,从而求得椭圆的标准方程;(2)方法一:直线
,从而求得椭圆的标准方程;(2)方法一:直线![]() 的斜率为
的斜率为![]() ,由
,由![]() 得直线
得直线![]() 的斜率为
的斜率为![]() ,即可分别表示出直线
,即可分别表示出直线![]() 和直线
和直线![]() 的方程,联立直线方程,得
的方程,联立直线方程,得![]() ,从而可得
,从而可得 ;方法二:设直线
;方法二:设直线![]() ,
, ![]() 的斜率为
的斜率为![]() ,
, ![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,由
,由![]() 得直线
得直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 的方程代入椭圆方程,从而求得
的方程代入椭圆方程,从而求得![]() ,再由
,再由![]() 在椭圆上,得
在椭圆上,得![]() 与
与![]() 的数量关系,从而表示出直线
的数量关系,从而表示出直线![]() 的方程,即可求得
的方程,即可求得![]() ,进而求得
,进而求得 .
.
试题解析:设![]() ,
, ![]() .
.
(1)在![]() 中,令
中,令![]() ,得
,得![]() ,从而b3.
,从而b3.
由 得
得![]() .
.
∴![]() .
.
∵![]()
∴![]() ,解得
,解得![]() .
.
∴椭圆的标准方程为![]() .
.
(2)方法一:
直线![]() 的斜率为
的斜率为![]() ,由
,由![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() .
.
于是直线![]() 的方程为:
的方程为: ![]() .
.
同理, ![]() 的方程为:
的方程为: ![]() .
.
联立两直线方程,消去y,得![]() .
.
∵![]() 在椭圆
在椭圆![]() 上
上
∴![]() ,从而
,从而![]() .
.
∴![]() .
.
∴ .
.
方法二:
设直线![]() ,
, ![]() 的斜率为k,
的斜率为k, ![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
由![]() 直线
直线![]() 的方程为
的方程为![]() .
.
将![]() 代入
代入![]() ,得
,得![]() ,
,
∵![]() 是椭圆上异于点
是椭圆上异于点![]() ,
, ![]() 的点
的点
∴![]() ,从而
,从而![]()
![]() .
.
∵![]() 在椭圆
在椭圆![]() 上
上
∴![]() ,从而
,从而![]() .
.
∴![]() ,得
,得![]() .
.
由![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() .
.
联立 则
则![]() ,即
,即![]() .
.
∴ .
.

 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案【题目】![]() 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国![]() 标准采用世界卫生组织设定的最宽限值,即
标准采用世界卫生组织设定的最宽限值,即![]() 日均值在
日均值在![]() 以下空气质量为优;在
以下空气质量为优;在![]() 之间空气质量为良;在
之间空气质量为良;在![]() 之间空气质量为轻度污染.某市环保局从该市2018年上半年每天的
之间空气质量为轻度污染.某市环保局从该市2018年上半年每天的![]() 日均值数据中随机抽取20天的数据作为样本,将
日均值数据中随机抽取20天的数据作为样本,将![]() 日均值统计如下:
日均值统计如下:
日均值( |
|
|
|
|
|
天数 | 4 | 6 | 5 | 3 | 2 |
(1)在空气质量为轻度污染的数据中,随机抽取两天![]() 日均值数据,求其中恰有一天
日均值数据,求其中恰有一天![]() 日均值数据在
日均值数据在![]() 之间的概率;
之间的概率;
(2)将以上样本数据绘制成频率分布直方图(直接作图):
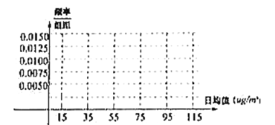
(3)该市规定:全年![]() 日均值的平均数不高于
日均值的平均数不高于![]() ,则认定该市当年的空气质量达标.现以这20天的
,则认定该市当年的空气质量达标.现以这20天的![]() 日均值的平均数来估计2018年的空气质量情况,试预测该市2018年的空气质量是否达标.
日均值的平均数来估计2018年的空气质量情况,试预测该市2018年的空气质量是否达标.


