题目内容
13.以下命题:①若x≠1或y≠2,则x+y≠3;
②若空间向量$\overrightarrow{OA}、\overrightarrow{OB}$与空间中任一向量都不能组成空间的一组基底,则$\overrightarrow{OA}$与$\overrightarrow{OB}$共线;
③若函数y=f(x)在x=x0处导数等于0,则该函数在该点处取得极值;
④若A、B为两个定点,K为正常数,若|PA|+|PB|=K,则动点P的轨迹是椭圆;
⑤已知抛物线y2=2px,以过焦点的一条弦AB为直径作圆,则此圆与准线相切;
其中真命题为②⑤.(写出所有真命题的序号)
分析 写出原命题的逆否命题,并判断真假,可判断①;根据基底的定义,可判断②;举出三次幂函数的反例,可判断③;根据椭圆的定义,可判断④;根据抛物线的性质,可判断⑤.
解答 解:对于①,若x≠1或y≠2,则x+y≠3的逆否命题为:若x+y=3,则x=1且y=2,为假命题,故①也为假命题;
对于②,若空间向量$\overrightarrow{OA}、\overrightarrow{OB}$与空间中任一向量都不能组成空间的一组基底,则$\overrightarrow{OA}$与$\overrightarrow{OB}$共线,故②正确;
对于③,若函数y=f(x)在x=x0处导数等于0,则该函数在该点处不一定取得极值,反例y=f(x)=x3,故③错误;
对于④,若A、B为两个定点,K为正常数,若|PA|+|PB|=K>|AB|,则动点P的轨迹是椭圆,
若|PA|+|PB|=K=|AB|,则动点P的轨迹是线段,故④错误;
对于⑤,已知抛物线y2=2px,以过焦点的一条弦AB为直径作圆,则圆心到准线的距离等于A,B两点到准线距离和的一半,
即圆心到准线的距离等于$\frac{1}{2}$|AB|=r,则此圆与准线相切,故⑤正确;
故真命题为:②⑤,
故答案为:②⑤.
点评 本题以命题的真假判断为载体,考查了四种命题,基底的定义,函数极值点的条件,椭圆的定义,抛物线的性质等知识点,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.f(x)=$\left\{\begin{array}{l}{x+2,}&{x≤-1}\\{{x}^{2},}&{-1<x<2}\\{2x,}&{x≥2}\end{array}\right.$,若f(x0)=3,则x0=( )
| A. | 3 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
2.将函数y=f(x)的图象先向左平移$\frac{π}{4}$个单位,然后向上平移1个单位,得到函数y=2cos2x的图象,则f(x-$\frac{7π}{2}$)是( )
| A. | -sin2x | B. | -2cosx | C. | 2sinx | D. | 2cosx |
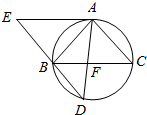 如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC. 过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3$\sqrt{5}$,BD=4则线段AF的长为$\frac{{5\sqrt{5}}}{3}$.
如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC. 过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB=AC,AE=3$\sqrt{5}$,BD=4则线段AF的长为$\frac{{5\sqrt{5}}}{3}$.