题目内容
2.设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),则$\sqrt{3}$PA+PB的最大值是2$\sqrt{10}$.分析 可得直线分别过定点(0,0)和(1,3)且垂直,可得|PA|2+|PB|2=10.三角换元后,由三角函数的知识可得$\sqrt{3}$PA+PB的最大值.
解答 解:由题意可得A(0,0),由于直线mx-y-m+3=0,即 m(x-1)-y+3=0,显然经过定点B(1,3),
注意到动直线x+my=0和动直线mx-y-m+3=0始终垂直,P又是两条直线的交点,
则有PA⊥PB,∴|PA|2+|PB|2=|AB|2=10.
设∠ABP=θ,则|PA|=$\sqrt{10}$sinθ,|PB|=$\sqrt{10}$cosθ.
∵|PA|≥0且|PB|≥0,可得θ∈[0,$\frac{π}{2}$],
∴$\sqrt{3}$|PA|+|PB|=$\sqrt{30}$sinθ+$\sqrt{10}$cosθ=2$\sqrt{10}$[$\frac{\sqrt{3}}{2}$sinθ+$\frac{1}{2}$cosθ)=2$\sqrt{10}$sin(θ+$\frac{π}{6}$),
∵θ∈[0,$\frac{π}{2}$],∴θ+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],∴当θ+$\frac{π}{6}$=$\frac{π}{2}$时,2$\sqrt{10}$sin(θ+$\frac{π}{6}$)取得最大值为 2$\sqrt{10}$,
故答案为:2$\sqrt{10}$.
点评 本题考查直线过定点问题,涉及直线的垂直关系和三角恒等变换,正弦函数的定义域和值域,属中档题.

练习册系列答案
相关题目
10.集合A={y|y=2x,x∈R},B={-1,0,1},则下列结论正确的是( )
| A. | A∪B=(0,+∞) | B. | (∁RA)∪B=(-∞,0] | C. | (∁RA)∩B={-1,0} | D. | (∁RA)∩B={1} |
17.小王有70元钱,现有面值分别为20元和30元的两种IC电话卡,若他至少买一张,则不同的买法共用( )
| A. | 7种 | B. | 8种 | C. | 6种 | D. | 9种 |
14.已知点P(x,y)是函数y=$\sqrt{-{x}^{2}+4x-3}$上的点,则$\frac{y+1}{x}$的取值范围是( )
| A. | (-∞,1] | B. | (-∞,$\frac{1}{3}$] | C. | (-∞,$\frac{1}{3}$]∪[1,+∞) | D. | [$\frac{1}{3}$,$\frac{4}{3}$] |
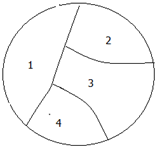 用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.
用五种不同的颜色给图中的四个区域涂色,每个区域涂一种颜色.