题目内容
7.已知p:$|x-\frac{3}{2}|≤\frac{7}{2}$,q:x2-4x+4-m2<0(m<0),若?p是?q的充分不必要条件,求实数m的取值范围.分析 分别化简p,q.?p是¬q的充分不必要条件,可得?p⇒?q,q⇒p.解出即可.
解答 解:若p为真,∵$|x-\frac{3}{2}|≤\frac{7}{2}$,∴$-\frac{7}{2}≤x-\frac{3}{2}$≤$\frac{7}{2}$,解得-2≤x≤5.
若q为真,则[x-(2+m)][x-(2-m)]<0,
∵m<0,∴2+m<2-m,
?p是¬q的充分不必要条件,
∴?p⇒?q,∴q⇒p.
$\left\{\begin{array}{l}2+m≥-2\\ 2-m≤5\end{array}\right.$,
∴m≥-3.
∴实数m的取值范围m≥-3.
点评 本题考查了充要条件的判定方法、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知集合M={x|0≤x≤2},N={x|x-2=0},则下列说法正确的是( )
| A. | N∈M | B. | N⊆M | C. | M⊆N | D. | M∈N |
15.已知定义域为R的函数f(x),对于x∈R,满足f[f(x)-x2+x]=f(x)-x2+x,设有且仅有一个实数x0,使得f(x0)=x0,则实数x0的值为( )
| A. | .0 | B. | .1 | C. | 0或1 | D. | .无法确定 |
2.下列命题中的假命题是( )
| A. | ?x0∈R,lgx0=0 | B. | ?x0∈R,tanx0=0 | C. | ?x∈R,x3>0 | D. | ?x∈R,2x>0 |
16.在半径为1的圆周上随机选取三点,它们构成一个锐角三角形的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
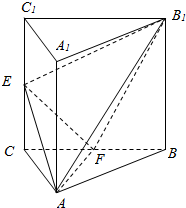 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1=2,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1=2,E,F分别是CC1,BC的中点.