题目内容
已知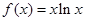 ,
,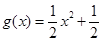 .
.
(1)设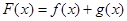 ,求函数
,求函数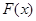 的图像在
的图像在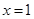 处的切线方程;
处的切线方程;
(2)求证: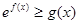 对任意的
对任意的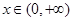 恒成立;
恒成立;
(3)若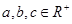 ,且
,且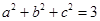 ,求证:
,求证: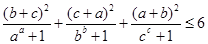 .
.
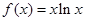 ,
,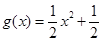 .
.(1)设
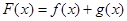 ,求函数
,求函数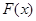 的图像在
的图像在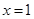 处的切线方程;
处的切线方程;(2)求证:
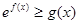 对任意的
对任意的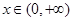 恒成立;
恒成立;(3)若
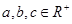 ,且
,且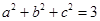 ,求证:
,求证: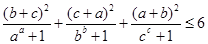 .
.(1)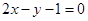 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
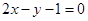 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.试题分析:(1)先求导函数
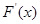 ,由导数的几何意义知,切线斜率为
,由导数的几何意义知,切线斜率为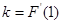 ,利用直线的点斜式方程可求;(2)构造函数
,利用直线的点斜式方程可求;(2)构造函数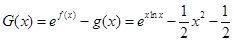 ,只需证明函数
,只需证明函数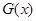 的最小值大于等于0即可,先求导得,
的最小值大于等于0即可,先求导得,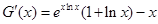 ,因导数等于0的根不易求出,再求导得,
,因导数等于0的根不易求出,再求导得,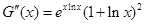
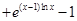 ,可判断
,可判断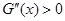 ,故
,故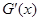 递增,且
递增,且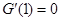 ,故
,故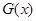 在
在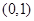 单调递减,在
单调递减,在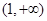 单调递增 ∴
单调递增 ∴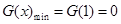 得证;(3)结合已知条件或已经得到的结论,得证明或判断的条件,是构造法求解问题的关键,由(2)知
得证;(3)结合已知条件或已经得到的结论,得证明或判断的条件,是构造法求解问题的关键,由(2)知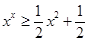 ,依次将代数式
,依次将代数式 放大,围绕目标从而证明不等式.
放大,围绕目标从而证明不等式.试题解析:(1)
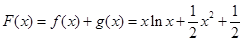 ,
,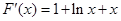 ,则
,则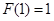
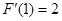 ,∴
,∴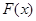 图像在
图像在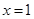 处的切线方程为
处的切线方程为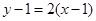 即
即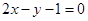 3分
3分(2)令
 ,
,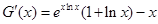 4分
4分则
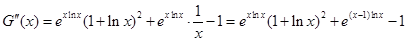
∵
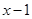 与
与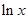 同号 ∴
同号 ∴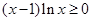 ∴
∴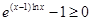
∴
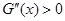 ∴
∴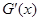 在
在 单调递增 6分
单调递增 6分又
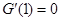 ,∴当
,∴当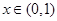 时,
时,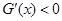 ;当
;当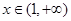 时,
时,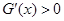
∴
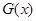 在
在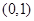 单调递减,在
单调递减,在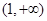 单调递增 ∴
单调递增 ∴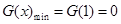
∴
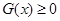 即
即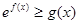 对任意的
对任意的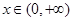 恒成立 8分
恒成立 8分(3)由(2)知
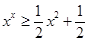 9分
9分则
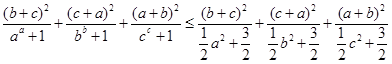
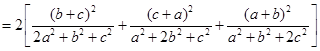 11分
11分由柯西不等式得
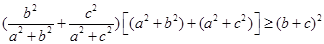
∴
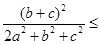
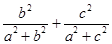 13分
13分同理
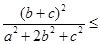
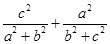
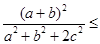
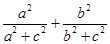
三个不等式相加即得证。 14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是定义在
是定义在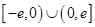 上的奇函数,当
上的奇函数,当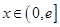 时,
时, 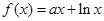 (其中e是自然界对数的底,
(其中e是自然界对数的底,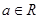 )
)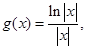 ,求证:当
,求证:当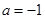 时,且
时,且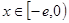 ,
, 恒成立;
恒成立;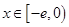 时,
时,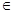 R).
R).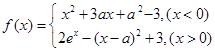 ,
,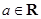 .
.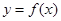 在
在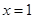 处取得极值,求
处取得极值,求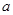 的值;
的值; ,
,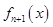 是
是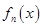 的导函数,即
的导函数,即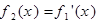 ,
,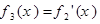 ,…,
,…,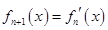 ,
,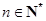 ,则
,则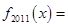 ( )
( )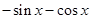
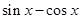
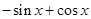
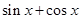
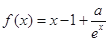 (
(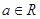 ,
,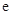 为自然对数的底数).
为自然对数的底数).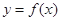 在点
在点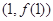 处的切线平行于
处的切线平行于 轴,求
轴,求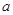 的值;
的值;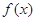 的极值;
的极值;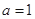 的值时,若直线
的值时,若直线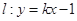 与曲线
与曲线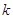 的最大值.
的最大值. 与函数
与函数 在点
在点 处有公共的切线,设
处有公共的切线,设
 .
. 的值
的值 在区间
在区间 上的最小值.
上的最小值.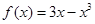 的单调减区间是
的单调减区间是