题目内容
14. 已知a,b,c分别为△ABC三个内角的对边,且a+b=$\sqrt{3}csinA+ccosA$.
已知a,b,c分别为△ABC三个内角的对边,且a+b=$\sqrt{3}csinA+ccosA$.(I)求角C;
(Ⅱ)如图,设D为BC的中点,且AD=2,求△ABC面积的最大值.
分析 (I)由正弦定理及三角函数恒等变换化简已知等式可得sin(C-$\frac{π}{6}$)=$\frac{1}{2}$,又结合C∈(0,π),即可求得角C的值;
(Ⅱ)由余弦定理结合已知可得$\frac{ab}{2}≤4$,又由三角形面积公式可得S△ABC=$\frac{1}{2}$ab•sinC=2$\sqrt{3}$.从而解得△ABC面积的最大值.
解答 解:(I)由正弦定理可得:sinA+sinB=$\sqrt{3}$sinCsinA+sinCcosA,又A+B+C=π,
∴sinA+sin(A+C)=$\sqrt{3}$sinCsinA+sinCcosA…3分
整理可得:1+cosC=$\sqrt{3}$sinC,
即:$\sqrt{3}$sinC-cosC=1,
有:sin(C-$\frac{π}{6}$)=$\frac{1}{2}$,…6分
又C∈(0,π),
∴C-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{5π}{6}$),
∴C-$\frac{π}{6}$=$\frac{π}{6}$,
∴C=$\frac{π}{3}$.…7分
(Ⅱ)如图,由余弦定理可得:AD2=CA2+CD2+2CA•CD•cosC=CA2+CD2-CA•CD=b2+$\frac{{a}^{2}}{4}$-$\frac{ab}{2}$=ab$-\frac{ab}{2}$=$\frac{ab}{2}$,…10分
∴$\frac{ab}{2}≤4$,…11分
又S△ABC=$\frac{1}{2}$ab•sinC=2$\sqrt{3}$.
∴△ABC面积的最大值是2$\sqrt{3}$.…12分
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式的应用,属于基本知识的考查.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 如图,在△ABC中,∠ACB=30°,点D在BC上,AD=BD=1,AB=$\sqrt{3}$,则∠BAC=( )
如图,在△ABC中,∠ACB=30°,点D在BC上,AD=BD=1,AB=$\sqrt{3}$,则∠BAC=( )| A. | 120° | B. | 150° | C. | 135° | D. | 90° |
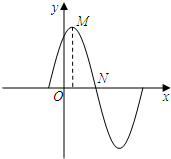 已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,其中M($\frac{π}{12}$,2),N($\frac{π}{3}$,0).
已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,其中M($\frac{π}{12}$,2),N($\frac{π}{3}$,0).