题目内容
19．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左焦点${F_1}（{-2\sqrt{5}，0}）$，右焦点${F_2}（{2\sqrt{5}，0}）$，离心率e=$\frac{{\sqrt{5}}}{2}$．若点P为双曲线C右支上一点，则|PF1|-|PF2|=8．分析 利用双曲线的焦点坐标以及离心率求出实半轴a，然后利用双曲线的定义求解即可．
解答 解：由题意c=2$\sqrt{5}$，∵e=$\frac{{\sqrt{5}}}{2}$．∴a=4，
由双曲线的定义可知|PF1|-|PF2|=2a=8．
故答案为：8．
点评 本题考查双曲线的定义以及双曲线的简单性质的应用，考查计算能力．
练习册系列答案
相关题目
9．若复数z满足z•（2-i）=1（i为虚数单位），则|z|=（ ）
| A． | $\frac{{\sqrt{5}}}{3}$ | B． | $\frac{1}{5}$ | C． | $\sqrt{5}$ | D． | $\frac{{\sqrt{5}}}{5}$ |
10．某全日制大学共有学生5400人，其中专科生有1500人，本科生有3000人，研究生有900人．现采用分层抽样的方法调查学生利用因特网查找学习资料的情况，抽取的样本为180人，则应在专科生、本科生与研究生这三类学生中分别抽取（ ）
| A． | 55人，80人，45人 | B． | 40人，100人，40人 | C． | 60人，60人，60人 | D． | 50人，100人，30人 |
已知a，b，c分别为△ABC三个内角的对边，且a+b=$\sqrt{3}csinA+ccosA$．
4．
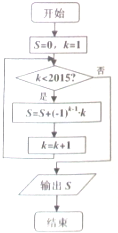阅读如图所示的框图，运行相应的程序，则输出S的值为（ ）
阅读如图所示的框图，运行相应的程序，则输出S的值为（ ）| A． | -1008 | B． | -1007 | C． | 1007 | D． | 1008 |