题目内容
从一副扑克牌的红桃花色中取5张牌,点数分别为1、2、3、4、5,甲、乙两人玩一种游戏:
甲先取一张牌,记下点数,放回后乙再取一张牌,记下点数.如果两个点数的和为偶数就算甲胜,否则算乙胜.
(Ⅰ)求甲胜且点数的和为6的事件发生的概率;
(Ⅱ)分别求出甲胜与乙胜的概率,判断这种游戏规则公平吗?
(Ⅰ)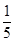 ;(Ⅱ)甲胜
;(Ⅱ)甲胜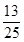 ,乙胜
,乙胜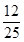 ,不公平。
,不公平。
解析试题分析:由已知可得,该游戏的基本事件有: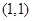 ,
,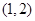 ,
,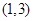 ,
,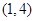 ,
,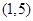 ,
, 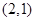 ,
,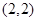 ,
,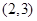 ,
,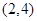 ,
,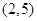 ,
, 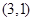 ,
,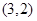 ,
, ,
,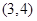 ,
,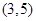 ,
, 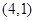 ,
,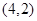 ,
,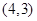 ,
,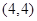 ,
, ,
, 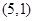 ,
,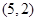 ,
,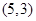 ,
,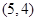 ,
,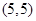 ,.......................3分
,.......................3分
(Ⅰ)记事件A:甲胜且点数的和为6,则
事件A包含的基本事件有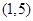 ,
,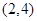 ,
, ,
,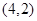 ,
,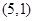
故事件A发生的概率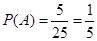 ...................6分
...................6分
(Ⅱ)记事件B:甲胜;记事件C:乙胜,则
事件B包含的基本事件有13种
事件C包含的基本事件有12种.........................9分
故事件B发生的概率为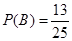
事件C发生的概率为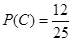 ............................11分
............................11分
综上所述,这个游戏规则不公平.................12分
考点:等可能事件的概率;古典概型的概率计算公式。
点评:本题考查等可能事件概率的计算,结合游戏的公平性,若双方取胜的概率相等,则游戏公平,反之,游戏不公平.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
(8分)对某校高一年级学生参加社区服务次数进行统计,随机抽取 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
 | 10 | 0.25 |
 | 25 |  |
 |  |  |
 | 2 | 0.05 |
| 合计 | M | 1 |

⑴求出表中
 、
、 及图中
及图中 的值;
的值;⑵若该校高一学生有720人,试估计他们参加社区服务的次数在区间
 内的人数;
内的人数;⑶在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
 内的概率.
内的概率. 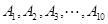 等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为
等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为 .
. 元,该同学决定按
元,该同学决定按 的分布列及数学期望.
的分布列及数学期望.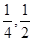 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为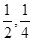 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。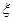 ,求
,求 .
. ,将赝品错误地鉴定为正品的概率为
,将赝品错误地鉴定为正品的概率为 ,已知一批物品共有4件,其中正品3件,赝品1件.(1)求该收藏爱好者的鉴定结果为正品2件,赝品2件的概率;(2)求该收藏爱好者的鉴定结果中正品数
,已知一批物品共有4件,其中正品3件,赝品1件.(1)求该收藏爱好者的鉴定结果为正品2件,赝品2件的概率;(2)求该收藏爱好者的鉴定结果中正品数 的分布列及数学期望.
的分布列及数学期望.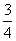 ,乙答对每个题的概率为
,乙答对每个题的概率为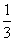 。
。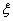 ,求
,求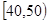 ,
,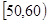 …
…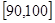 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题: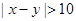 ”的概率.
”的概率.
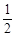 ,乙射击一次中靶概率是
,乙射击一次中靶概率是 ,
,