题目内容
（本小题12分）已知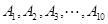
等10所高校举行的自主招生考试，某同学参加每所高校的考试获得通过的概率均为
.
（Ⅰ）如果该同学10所高校的考试都参加，试求恰有2所通过的概率；
（Ⅱ）假设该同学参加每所高校考试所需的费用均为
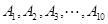元，该同学决定按顺序参加考试，一旦通过某所高校的考试，就不再参加其它高校的考试，试求该同学参加考试所需费用
的分布列及数学期望.
（1）
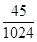（2）
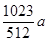
解析试题分析：．解（Ⅰ）因为该同学通过各校考试的概率均为 一家化妆品公司于今年三八节期间在某社区举行了为期三天的“健康使用化妆品知识讲座”．每位社区居民可以在这三天中的任意一天参加任何一个讨论，也可以放弃任何一个讲座（规定：各个讲座达到预先设定的人数时称为满座）．统计数据表明，各个讲座各天满座的概率如下表：，所以该同学恰好通过2所高校自主招生考试的概率为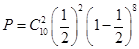
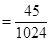. ………………4分
（Ⅱ）设该同学共参加了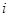
次考试的概率为
（
）.
∵
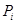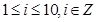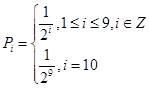， ……………………6分
∴所以该同学参加考试所需费用的分布列如下：2 3 4 5 6 7 8 9 10 
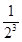
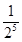
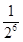
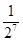
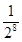
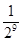
创新金卷毕业升学系列答案
创新课时训练系列答案
创新学案课时学练测系列答案
创新学习三级训练系列答案
创新与探究系列答案
达标测试卷系列答案
达标训练系列答案
打好基础课堂10分钟系列答案
大联考单元期末测试卷系列答案
大赢家考前巧复习系列答案
（1）求面膜使用讲座三天都不满座的概率；
洗发水讲座
洗面奶讲座
护肤霜讲座
活颜营养讲座
面膜使用讲座
3月8日
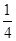
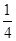
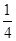
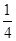
3月9日
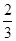
3月10日
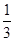
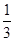
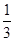
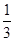
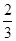
（2）设3月9日各个讲座满座的数目为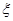
，求随机变量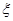的分布列和数学期望．
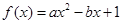，分别从集合P和Q中随机取一个数a和b得到数列
。
，
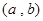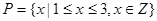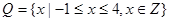，列举出所有的数对
有零点的概率；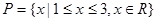
，
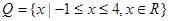，求函数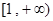
上是增函数的概率。
的
，已知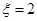
时，共有6种坐法．
在R上不存在极值点的概率；
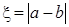，求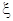
的分布列和数学期望.
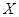，求
．