题目内容
已知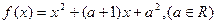 ,若
,若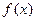 能表示成一个奇函数
能表示成一个奇函数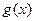 和一个偶函数
和一个偶函数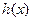 的和.
的和.
(Ⅰ)求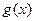 和
和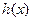 的解析式;
的解析式;
(Ⅱ)若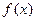 和
和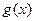 在区间
在区间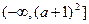 上都是减函数,求
上都是减函数,求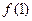 的取值范围.
的取值范围.
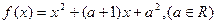 ,若
,若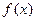 能表示成一个奇函数
能表示成一个奇函数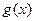 和一个偶函数
和一个偶函数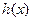 的和.
的和.(Ⅰ)求
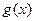 和
和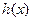 的解析式;
的解析式;(Ⅱ)若
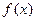 和
和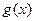 在区间
在区间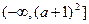 上都是减函数,求
上都是减函数,求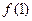 的取值范围.
的取值范围.(Ⅰ)
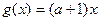 ,
,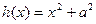
(Ⅱ)
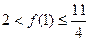
解:(I)由题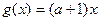 ,
,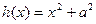 ;(写出答案就给满分)--------4分
;(写出答案就给满分)--------4分
(II)因为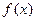 和
和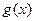 在区间
在区间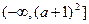 上都是减函数,
上都是减函数,
所以 ,即
,即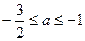
且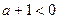 ,即
,即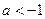
从而 ------------- ---9分
------------- ---9分
又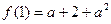 ,可看成是关于变量
,可看成是关于变量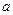 的函数
的函数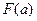 ,并
,并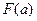 在区间
在区间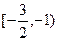 上单调递减,所以
上单调递减,所以 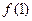 的取值范围为
的取值范围为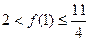 -----------------------14分
-----------------------14分
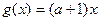 ,
,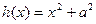 ;(写出答案就给满分)--------4分
;(写出答案就给满分)--------4分(II)因为
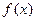 和
和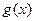 在区间
在区间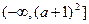 上都是减函数,
上都是减函数,所以
 ,即
,即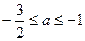
且
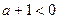 ,即
,即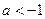
从而
 ------------- ---9分
------------- ---9分
又
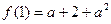 ,可看成是关于变量
,可看成是关于变量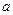 的函数
的函数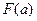 ,并
,并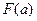 在区间
在区间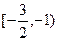 上单调递减,所以
上单调递减,所以 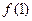 的取值范围为
的取值范围为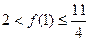 -----------------------14分
-----------------------14分
练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
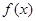 在定义域R上不是常数函数,且
在定义域R上不是常数函数,且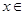 R,
R,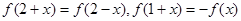 ,则
,则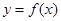 是偶函数,当
是偶函数,当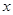 >0 时,
>0 时,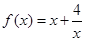 ,且当
,且当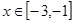 时,
时,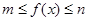 成立,则
成立,则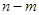 的最小值为
的最小值为 B.
B.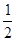 C.
C. 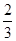 D. 1
D. 1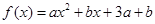 是偶函数,且定义域为
是偶函数,且定义域为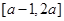 ,则
,则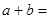 _______
_______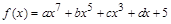 ,其中
,其中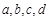 为常数,若
为常数,若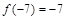 ,则
,则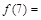 _____
_____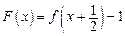 是R上的奇函数,
是R上的奇函数,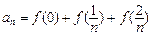
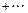
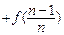
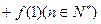 ,则数列
,则数列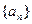 的通项公式为 ( )
的通项公式为 ( )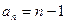
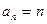
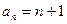
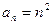
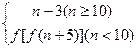 ,其中n∈N,则f(8)等于
,其中n∈N,则f(8)等于 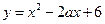 是偶函数,则
是偶函数,则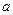 的值是 .
的值是 .