题目内容
13.已知函数f(x)=$\frac{2}{{2}^{x}+1}$-2+log3($\sqrt{{x}^{2}+9}$-x),a=-f(cos($\frac{3π}{2}$-3)),b=-f(log3$\frac{1}{2}$),c=f(log43),则( )| A. | c>b>a | B. | b>c>a | C. | a>c>b | D. | a>b>c |
分析 先判断函数f(x)是R上的奇偶性与单调性.可得:a=f(sin3),b=f(log32),c=f(log43),又0<sin3<$\frac{1}{2}=lo{g}_{3}\sqrt{3}$<log32$<\frac{2}{3}$<log43<1,即可得出.
解答 解:函数f(x)=$\frac{2}{{2}^{x}+1}$-2+log3($\sqrt{{x}^{2}+9}$-x)=$\frac{2}{{2}^{x}+1}$-2+$lo{g}_{3}\frac{9}{\sqrt{{x}^{2}+9}+x}$,x∈R.
∴f(-x)+f(x)=$\frac{2}{{2}^{-x}+1}-2$+$lo{g}_{3}\frac{9}{\sqrt{{x}^{2}+9}-x}$+$\frac{2}{{2}^{x}+1}$-2+$lo{g}_{3}\frac{9}{\sqrt{{x}^{2}+9}+x}$=0,即f(-x)=-f(x),x∈R.
∴函数f(x)是奇函数.
当x>0时,由于y=$\frac{2}{{2}^{x}+1}$单调递减,y=$lo{g}_{3}\frac{9}{\sqrt{{x}^{2}+9}+x}$也单调递减,∴函数f(x)在x>0时单调递减.
可得函数f(x)在x∈R时单调递减.
∵$cos(\frac{3π}{2}-3)$=-sin3,$lo{g}_{3}\frac{1}{2}$=-log32,
∴a=f(sin3),b=f(log32),c=f(log43).
∵0<sin3<$\frac{1}{2}=lo{g}_{3}\sqrt{3}$<log32$<\frac{2}{3}$<log43<1,
∴a>b>c.
故选:D.
点评 本题考查了函数的奇偶性与单调性,考查了推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案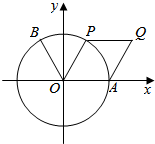 如图,点B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),点A时单位圆与x轴正半轴的交点.设点P为单位圆上的动点,点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$,∠AOP=2θ($\frac{π}{6}$≤θ<$\frac{π}{2}$),f(θ)=$\overrightarrow{OB}$•$\overrightarrow{OQ}$,求f(θ)的取值范围,当$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$时,求四边形OAQP的面积.
如图,点B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),点A时单位圆与x轴正半轴的交点.设点P为单位圆上的动点,点Q满足$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$,∠AOP=2θ($\frac{π}{6}$≤θ<$\frac{π}{2}$),f(θ)=$\overrightarrow{OB}$•$\overrightarrow{OQ}$,求f(θ)的取值范围,当$\overrightarrow{OB}$⊥$\overrightarrow{OQ}$时,求四边形OAQP的面积.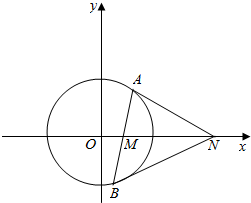 如图,已知圆O:x2+y2=r2(r>0),动直线l过点M(1,0)交圆O于A(x1,y1),B(x2,y2)两点(点A在x轴上方),点N在x轴上,若点B的坐标为(0,-r),则点A的横坐标为$\frac{8}{5}$.
如图,已知圆O:x2+y2=r2(r>0),动直线l过点M(1,0)交圆O于A(x1,y1),B(x2,y2)两点(点A在x轴上方),点N在x轴上,若点B的坐标为(0,-r),则点A的横坐标为$\frac{8}{5}$.