题目内容
【题目】设锐角三角形
的内角
的对边分别为
， 
．
（Ⅰ）求
的大小；
（Ⅱ）求
的取值范围．
【答案】解：（1）由
，根据正弦定理得
， ………2分
所以
，由
为锐角三角形得
． ………………4分
（2）
． ……………………………8分
由
为锐角三角形知， 
， 
．
，所以
． ……………………………11分
由此有
，
所以， 
的取值范围为
． ……………………………12分
【解析】试题分析：（1）由
，根据正弦定理得
，所以
，由
为锐角三角形得
；（2）由（1）知
，利用诱导公式与辅助角公式变形化简得
，由
为锐角三角形知
，因此
的取值范围为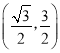
．
试题解析：（1）由
，根据正弦定理得
，所以
，
由
为锐角三角形得
．
（2）
．
由
为锐角三角形知， 
，
所以
．由此有
，
所以， 
的取值范围为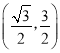
．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
