题目内容
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,过
,过![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,当直线
,当直线![]() 的倾斜角是
的倾斜角是![]() 时,
时, ![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() .
.

(1)求![]() 的值;
的值;
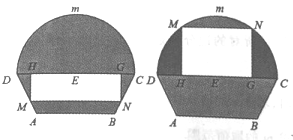
(2)以![]() 为直径的圆交
为直径的圆交![]() 轴于点
轴于点![]() ,记劣弧
,记劣弧![]() 的长度为
的长度为![]() ,当直线
,当直线![]() 绕
绕![]() 点旋转时,求
点旋转时,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)设出直线![]() 的方程为
的方程为![]() ,设
,设![]() ,联立直线与抛物线方程,利用韦达定理求出
,联立直线与抛物线方程,利用韦达定理求出![]() 中点坐标,推出中垂线方程,结合
中点坐标,推出中垂线方程,结合![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() ,求出
,求出![]() 即可;(2)设
即可;(2)设![]() 方程为
方程为![]() ,代入
,代入![]() ,求出
,求出![]() 的距离以及
的距离以及![]() 中点为
中点为![]() ,令
,令![]() ,求出
,求出![]() 的表达式,推出关系式
的表达式,推出关系式![]() ,利用
,利用![]() 到
到![]() 轴的距离
轴的距离![]() ,求出
,求出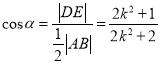 ,分离常数即可求得
,分离常数即可求得![]() 的最大值.
的最大值.
试题解析:(1)![]() 当
当![]() 的倾斜角为
的倾斜角为![]() 时,
时, ![]() 的方程为
的方程为![]()
设![]()
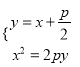 得
得![]()
![]() 得
得![]() 中点为
中点为![]()
![]() 中垂线为
中垂线为![]()
![]() 代入得
代入得![]()
![]()
(2)设![]() 的方程为
的方程为![]() ,代入
,代入![]() 得
得![]()
![]()
![]() 中点为
中点为![]()
令![]()
![]()
![]()
![]() 到
到![]() 轴的距离
轴的距离![]()
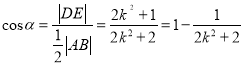
当![]() 时
时![]() 取最小值
取最小值![]()
![]() 的最大值为
的最大值为![]()
故![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了![]() 人,他们年龄大点频数分布及支持“生育二胎”人数如下表:
人,他们年龄大点频数分布及支持“生育二胎”人数如下表:
年龄 |
|
|
|
|
|
| ||
频数 |
|
|
|
|
|
| ||
支持“生育二胎” |
|
|
|
|
|
| ||
(Ⅰ)由以上统计数据填下面 | 年龄不低于 | 年龄低于 | 合计 | |||||
支持 |
|
| ||||||
不支持 |
|
| ||||||
合计 | ||||||||
(Ⅱ)若对年龄在![]() 的的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
参考数据: ![]() ,
, ![]() .
.