Question

【题目】已知函数，其中=2.71828…为自然数的底数.

（1）当时，讨论函数的单调性；

（2）当时，求证：对任意的， .

Answer 1

【答案】(1)f（x）在R上单调递减.(2)证明见解析.

【解析】试题分析：（1）求函数的导数，利用函数单调性和导数之间的关系进行讨论即可；（2）对任意的x∈[0，+∞），转化为证明对任意的x∈[0，+∞），，即可，构造函数，求函数的导数，利用导数进行研究即可．

试题解析：（1）当a=0时，f（x）=ex（sinx﹣e），

则f′（x）=ex（sinx﹣e）+excosx=ex（sinx﹣e+cosx），

∵sinx+cosx= 、

∴sinx+cosx﹣e＜0

故f′（x）＜0

则f（x）在R上单调递减.

（2）当x≥0时，y=ex≥1，

要证明对任意的x∈[0，+∞），f（x）＜0.

则只需要证明对任意的x∈[0，+∞），

设g（a）=sinx﹣ax2+2a﹣e=（﹣x2+2）a+sinx﹣e，

看作以a为变量的一次函数，

要使sinx﹣ax2+2a﹣e＜0，

则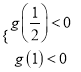，即，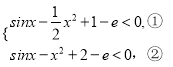

∵sinx+1﹣e＜0恒成立，∴①恒成立，

对于②，令h（x）=sinx﹣x2+2﹣e，

则h′（x）=cosx﹣2x，

设x=t时，h′（x）=0，即cost﹣2t=0.

∴t=，sint＜

∴h（x）在（0，t）上，h′（x）＞0，h（x）单调递增，在（t，+∞）上，h′（x）＜0，h（x）单调递减，

则当x=t时，函数h（x）取得最大值h（t）=sint﹣t2+2﹣e=sint﹣（）2+2﹣e

=sint﹣+2﹣e=sin2t+sint+﹣e=（+1）2+﹣e≤（）2+﹣e=﹣e＜0，

故④式成立，

综上对任意的x∈[0，+∞），f（x）＜0.