[题目]已知函数.其中是实数.设. 为该函数图象上的两点.且.(1)若函数的图象在点处的切线互相垂直.且.求的最小值,(2)若函数的图象在点处的切线重合.求的取值范围. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知函数，其中是实数。设，为该函数图象上的两点，且.

（1）若函数的图象在点处的切线互相垂直，且，求的最小值；

（2）若函数的图象在点处的切线重合，求的取值范围.

【答案】（1）；（2）

【解析】试题分析：（1）利用导数的几何意义即可得到切线的斜率，因为切线互相垂直，可得，即．可得，再利用基本不等式的性质即可得出；（2）当或时，∵，故不成立，∴，分别写出切线的方程，根据两条直线重合的充要条件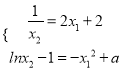即可得出，记再利用导数即可得出．

试题解析：(1)由导数的几何意义可知，点处的切线斜率为，点处的切线斜率为，故当处的切线与处的切线垂直时，，当时，有，所以，，所以，所以，当且仅当，即，时，等号成立，所以的最小值为.

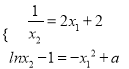（2）当或时，，所以，当时，函数图象在点处的切线方程为，即，当时，函数图象在点处的切线方程为，即，两处切线重合的充要条件是，由及，得，，记，则，所以在单调递减，，趋近于时，趋近于，所以，所以的取值范围是.

练习册系列答案

相关题目

【题目】已知抛物线的焦点为F,直线与x轴的交点为P,与抛物线的交点为Q,且 .
（1）求抛物线的方程;
（2）过F的直线l与抛物线相交于A,D两点,与圆相交于B,C两点(A,B两点相邻),过A,D两点分别作抛物线的切线,两条切线相交于点M,求△ABM与△CDM的面积之积的最小值.

【题目】已知函数f(x)=sin(cosx)-x与函数g(x)=cos(sinx)-x在区间(0， )都为减函数，设x1,x2,x3∈(0， )，且cosx1=x1 ， sin(cosx2)=x2 ， cos(sinx3)=x3 ，则x1,x2,x3的大小关系是（）
A.x1<x2<x3
B.x3<x1<x2
C.x2<x1<x3
D.x2<x3<x1

【题目】（本小题满分12分）已知函数，( 为常数)．

（1）求函数在点 (，)处的切线方程；

（2）当时，设，若函数在定义域上存在单调减区间，求实数的取值范围；

【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度，现在某市进行调查，随机调查了人，他们年龄大点频数分布及支持“生育二胎”人数如下表：

年龄
频数
支持“生育二胎”
（Ⅰ）由以上统计数据填下面乘列联表，并问是否有的把握认为以岁为分界点对“生育二胎放开”政策的支持度有差异：	年龄不低于岁的人数	年龄低于岁的人数	合计
支持
不支持
合计