Question

14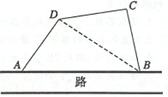．如图，在一条直路边上有相距100$\sqrt{3}$米的A、B两定点，路的一侧是一片荒地，某人用三块长度均为100米的篱笆（不能弯折），将荒地围成一块四边形地块ABCD（直路不需要围），经开垦后计划在三角形地块ABD和三角形地块BCD分别种植甲、乙两种作物．已知两种作物的年收益都与各自地块的面积的平方成正比，且比例系数均为k（正常数），设∠DAB=α．
（1）当α=60°时，若要用一块篱笆将上述两三角形地块隔开，现有篱笆150米，问是否够用，说明理由？
（2）求使两块地的年总收益最大时，角α的余弦值？

Answer 1

分析 （1）运用余弦定理，求得BD，再与150比较，即可得到；
（2）运用三角形的面积公式，求得△ABD的面积，求得BD，由等腰三角形的面积公式可得△BCD的面积，再与同角的平方关系，结合配方和二次函数的值域求法，即可得到最大值

解答 解：（1）在△ABD中，AB=100$\sqrt{3}$，AB=100，∠DAB=60°，
则BD²=100²+（100$\sqrt{3}$）²-2×100×100$\sqrt{3}$×cos60°
=4×100²-100²×$\sqrt{3}$，
即为BD=100$\sqrt{4-\sqrt{3}}$＞150，
则不够用；
（2）设甲种作物的年收益为y₁，则y₁=kS²_△ABD，
乙种作物的年收益为y₂，则y₁=kS²_△CBD，
总收益为y，y=y₁+y₂，
在△ABD中，S_△ABD=$\frac{1}{2}$×100×100$\sqrt{3}$sinα=
又BD²=100²+（100$\sqrt{3}$）²-2×100×100$\sqrt{3}$×cosα
=4×100²-100²×2$\sqrt{3}$cosα，
△BCD的边BD上的高为h=$\sqrt{10{0}^{2}-\frac{4×10{0}^{2}-10{0}^{2}×2\sqrt{3}cosα}{4}}$
=50$\sqrt{2\sqrt{3}cosα}$，
则S_△BCD=$\frac{1}{2}$×50$\sqrt{2\sqrt{3}cosα}$×100$\sqrt{4-2\sqrt{3}cosα}$，
即有S=k[$\frac{1}{4}$×100⁴×3sin²α+$\frac{1}{4}$×50²×100²×4$\sqrt{3}$（2-$\sqrt{3}$cosα）cosα]
=$\frac{1}{4}$×10⁸k（3sin²α-3cos²α+2$\sqrt{3}$cosα）
=$\frac{1}{4}$×10⁸k（-6cos²α+2$\sqrt{3}$cosα+3）
=$\frac{1}{4}$×10⁸k[-6（cosα-$\frac{\sqrt{3}}{6}$）²+$\frac{7}{2}$]，
故当cosα=$\frac{\sqrt{3}}{6}$时，两块地的年总收益最大，且为$\frac{7}{8}$×10⁸k．

点评 本题考查解三角形的应用题，考查余弦定理和面积公式的运用，同时考查三角函数的化简和求最值，注意运用二次函数的最值求法，属于中档题．