题目内容
6.解方程组:$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=5}\\{{2x}^{2}-3xy-2{y}^{2}=0}\end{array}\right.$.分析 由②得:(2x+y)(x-2y)=0,即2x+y=0或x-2y=0,分类讨论利用代入消元法,可得答案.
解答 解:$\left\{\begin{array}{l}{x}^{2}+{y}^{2}=5①\\{2x}^{2}-3xy-2{y}^{2}=0②\end{array}\right.$
由②得:(2x+y)(x-2y)=0,
即2x+y=0或x-2y=0,
当2x+y=0,即y=-2x时,
代入①得:5x2=5,
解得:$\left\{\begin{array}{l}x=1\\ y=-2\end{array}\right.$,或$\left\{\begin{array}{l}x=-1\\ y=2\end{array}\right.$,
当x-2y=0,即x=2y时,
代入①得:5y2=5,
解得:$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$,或$\left\{\begin{array}{l}x=-2\\ y=-1\end{array}\right.$,
综上所述,方程组:$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=5}\\{{2x}^{2}-3xy-2{y}^{2}=0}\end{array}\right.$的解有$\left\{\begin{array}{l}x=1\\ y=-2\end{array}\right.$,或$\left\{\begin{array}{l}x=-1\\ y=2\end{array}\right.$,或$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$,或$\left\{\begin{array}{l}x=-2\\ y=-1\end{array}\right.$,
点评 本题考查的知识点是二元二次方程组的解法,利用因式分解法进行降次,利用代入法或加减法进行消元是常用的方法.

| A. | [-$\frac{5}{4}$,0) | B. | (0,+∞) | C. | [-$\frac{5}{4}$,0)∪(0,+∞) | D. | [-$\frac{5}{4}$,0)∪[$\frac{5}{4}$,+∞) |
| A. | 0∈{(0,1)} | B. | 1∈{(0,1)} | C. | (0,1)∈{(0,1)} | D. | (0,1)∈{0,1} |
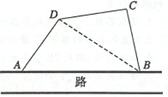 如图,在一条直路边上有相距100$\sqrt{3}$米的A、B两定点,路的一侧是一片荒地,某人用三块长度均为100米的篱笆(不能弯折),将荒地围成一块四边形地块ABCD(直路不需要围),经开垦后计划在三角形地块ABD和三角形地块BCD分别种植甲、乙两种作物.已知两种作物的年收益都与各自地块的面积的平方成正比,且比例系数均为k(正常数),设∠DAB=α.
如图,在一条直路边上有相距100$\sqrt{3}$米的A、B两定点,路的一侧是一片荒地,某人用三块长度均为100米的篱笆(不能弯折),将荒地围成一块四边形地块ABCD(直路不需要围),经开垦后计划在三角形地块ABD和三角形地块BCD分别种植甲、乙两种作物.已知两种作物的年收益都与各自地块的面积的平方成正比,且比例系数均为k(正常数),设∠DAB=α.