题目内容
9.已知数列{an}的首项a1=a,an =$\frac{1}{2}$an-1+1(n∈N*,n≥2),bn=an-2(n∈N*).(1)问数列{bn}是否构成等比数列;
(2)若已知a=1,设cn=bn (bn +$\frac{2}{3}$),试探究数列{cn}是否存在最大项和最小项?若存在求出最大项和最小项对应的n值,若不存在,说明理由;
(3)若已知a=1,设dn=n2-2n+t(n∈N+,t是常变量),若对任意n,k∈N*,不等式dk+n•bn≥0恒成立,求实数t的取值范围.
分析 (1)由递推式可得b1=a1-2,an=bn+2,进一步得到${b}_{n}=\frac{1}{2}{b}_{n-1}$,然后分a≠2和a=2讨论得答案;
(2)当a=1时,求得${b}_{n}=-(\frac{1}{2})^{n-1}$,代入cn=bn (bn +$\frac{2}{3}$)后化简,令m=$(\frac{1}{2})^{n-1}$,然后利用二次函数的最值得答案;
(3)a=1时,${b}_{n}=-(\frac{1}{2})^{n-1}$,对任意n,k∈N*,不等式dk+n•bn≥0恒成立,即k2-2k+t-$n•(\frac{1}{2})^{n-1}≥0$恒成立,也即k2-2k+t≥$n•(\frac{1}{2})^{n-1}$恒成立,分离变量t后由函数的单调性求得实数t的取值范围.
解答 解:(1)b1=a1-2,an=bn+2.
∴bn+2=$\frac{1}{2}$(bn-1+2)+1,${b}_{n}=\frac{1}{2}{b}_{n-1}$,
∴当a≠2时,数列bn构成等比数列.
当a=2时,数列bn不构成等比数列;
(2)当a=1,得b1=-1,${b}_{n}=-(\frac{1}{2})^{n-1}$,
cn=bn (bn +$\frac{2}{3}$)=$-(\frac{1}{2})^{n-1}[\frac{2}{3}-(\frac{1}{2})^{n-1}]$=$[(\frac{1}{2})^{n-1}]^{2}-\frac{2}{3}(\frac{1}{2})^{n-1}$.
令m=$(\frac{1}{2})^{n-1}$,则当m=1,即n=1时,cn有最大项为${c}_{1}=\frac{1}{3}$,
当n=3时,cn有最小项为${c}_{3}=-\frac{5}{48}$;
(3)∵a=1,∴${b}_{n}=-(\frac{1}{2})^{n-1}$,
对任意n,k∈N*,不等式dk+n•bn≥0恒成立,即k2-2k+t-$n•(\frac{1}{2})^{n-1}≥0$恒成立,
也即k2-2k+t≥$n•(\frac{1}{2})^{n-1}$恒成立,
∴t≥$n•(\frac{1}{2})^{n-1}$+1恒成立,
∵$\frac{(n+1)•(\frac{1}{2})^{n}}{n•(\frac{1}{2})^{n-1}}$=$\frac{n+1}{2n}≤1$,
∴函数f(n)=$n•(\frac{1}{2})^{n-1}$+1为减函数,则f(n)min=2.
∴t≥2.
点评 本题主要考查了等比数列的性质,等比数列的通项公式运用.考查了学生综合运用等比数列的基础知识的能力,考查数列的函数特性,是中档题.

| A. | (-∞,-1) | B. | (-1,+∞) | C. | (-∞,-$\frac{1}{2}$) | D. | (-$\frac{1}{2}$,+∞) |
| A. | [-$\frac{5}{4}$,0) | B. | (0,+∞) | C. | [-$\frac{5}{4}$,0)∪(0,+∞) | D. | [-$\frac{5}{4}$,0)∪[$\frac{5}{4}$,+∞) |
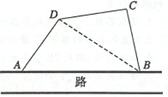 如图,在一条直路边上有相距100$\sqrt{3}$米的A、B两定点,路的一侧是一片荒地,某人用三块长度均为100米的篱笆(不能弯折),将荒地围成一块四边形地块ABCD(直路不需要围),经开垦后计划在三角形地块ABD和三角形地块BCD分别种植甲、乙两种作物.已知两种作物的年收益都与各自地块的面积的平方成正比,且比例系数均为k(正常数),设∠DAB=α.
如图,在一条直路边上有相距100$\sqrt{3}$米的A、B两定点,路的一侧是一片荒地,某人用三块长度均为100米的篱笆(不能弯折),将荒地围成一块四边形地块ABCD(直路不需要围),经开垦后计划在三角形地块ABD和三角形地块BCD分别种植甲、乙两种作物.已知两种作物的年收益都与各自地块的面积的平方成正比,且比例系数均为k(正常数),设∠DAB=α.