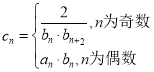题目内容
【题目】已知函数![]() 且在
且在![]() 上的最大值为
上的最大值为![]() ,
,
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,π)内的零点个数,并加以证明
【答案】(1)![]() (2)2个零点.
(2)2个零点.
【解析】
(1)由题意,可借助导数研究函数![]() 上的单调性,确定出最值,令最值等于
上的单调性,确定出最值,令最值等于![]() ,即可得到关于a的方程,由于a的符号对函数的最值有影响,故可以对a的取值范围进行讨论,分类求解;(2)借助导数研究函数f(x)在(0,π)内单调性,由零点判定定理即可得出零点的个数.
,即可得到关于a的方程,由于a的符号对函数的最值有影响,故可以对a的取值范围进行讨论,分类求解;(2)借助导数研究函数f(x)在(0,π)内单调性,由零点判定定理即可得出零点的个数.
(1)由已知得f′(x)=a(sinx+xcosx),对于任意的x∈(0, ![]() ),
),
有sinx+xcosx>0,当a=0时,f(x)= ![]() ,不合题意;
,不合题意;
当a<0时,x∈(0,![]() ),f′(x)<0,从而f(x)在(0,
),f′(x)<0,从而f(x)在(0, ![]() )单调递减,
)单调递减,
又函数f(x)=axsinx![]() (a∈R)在[0,
(a∈R)在[0, ![]() ]上图象是连续不断的,
]上图象是连续不断的,
故函数在[0, ![]() ]上的最大值为f(0),不合题意;
]上的最大值为f(0),不合题意;
当a>0时,x∈(0, ![]() ),f′(x)>0,从而f(x)在(0,
),f′(x)>0,从而f(x)在(0, ![]() )单调递增,
)单调递增,
又函数f(x)=axsinx ![]() (a∈R)在[0,
(a∈R)在[0, ![]() ]上图象是连续不断的,
]上图象是连续不断的,
故函数在[0, ![]() ]上上的最大值为f(
]上上的最大值为f(![]() )=
)=![]() a
a![]() =
=![]() ,解得a=1,
,解得a=1,
综上所述,得![]() ;
;
(2)函数f(
由(I)知,f(x)=xsinx![]() ,从而有f(0)=
,从而有f(0)= ![]() <0,f(
<0,f(![]() )=π32>0,
)=π32>0,
又函数在[0, ![]() ]上图象是连续不断的,所以函数f(x)在(0,
]上图象是连续不断的,所以函数f(x)在(0, ![]() )内至少存在一个零点,
)内至少存在一个零点,
又由(I)知f(x)在(0, ![]() )单调递增,故函数f(x)在(0,
)单调递增,故函数f(x)在(0, ![]() )内仅有一个零点。
)内仅有一个零点。
当x∈[![]() ,π]时,令g(x)=f′(x)=sinx+xcosx,
,π]时,令g(x)=f′(x)=sinx+xcosx,
由g(![]() )=1>0,g(π)=π<0,且g(x)在[
)=1>0,g(π)=π<0,且g(x)在[![]() ,π]上的图象是连续不断的,
,π]上的图象是连续不断的,
故存在m∈![]() ,π),使得g(m)=0.
,π),使得g(m)=0.
由g′(x)=2cosxxsinx,知x∈(![]() ,π)时,有g′(x)<0,
,π)时,有g′(x)<0,
从而g(x)在[![]() ,π]上单调递减。
,π]上单调递减。
当x∈![]() ,m),g(x)>g(m)=0,即f′(x)>0,
,m),g(x)>g(m)=0,即f′(x)>0,
从而f(x)在(![]() ,m)内单调递增
,m)内单调递增
故当x∈(![]() ,m)时,f(x)>f(π2)=π32>0,
,m)时,f(x)>f(π2)=π32>0,
从而(x)在(![]() ,m)内无零点;
,m)内无零点;
当x∈(m,π)时,有g(x)<g(m)=0,即f′(x)<0,
从而f(x)在(![]() ,m)内单调递减。
,m)内单调递减。
又f(m)>0,f(π)<0且f(x)在[m,π]上的图象是连续不断的,
从而f(x)在[m,π]内有且仅有一个零点。
综上所述,函数f(x)在(0,π)内有且仅有两个零点。