题目内容
已知函数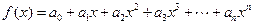 (n∈N+),且y=f(x)的图象经过点(1,n2),数列{an}(n∈N+)为等差数列.(1)求数列{ an}的通项公式;
(n∈N+),且y=f(x)的图象经过点(1,n2),数列{an}(n∈N+)为等差数列.(1)求数列{ an}的通项公式;
(2)当n为奇函数时,设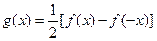 ,是否存在自然数m和M,使不等式m<
,是否存在自然数m和M,使不等式m<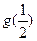 <M恒成立,若存在,求出M-m的最小值;若不存在,说明理由.
<M恒成立,若存在,求出M-m的最小值;若不存在,说明理由.
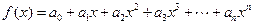 (n∈N+),且y=f(x)的图象经过点(1,n2),数列{an}(n∈N+)为等差数列.(1)求数列{ an}的通项公式;
(n∈N+),且y=f(x)的图象经过点(1,n2),数列{an}(n∈N+)为等差数列.(1)求数列{ an}的通项公式;(2)当n为奇函数时,设
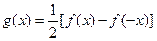 ,是否存在自然数m和M,使不等式m<
,是否存在自然数m和M,使不等式m<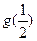 <M恒成立,若存在,求出M-m的最小值;若不存在,说明理由.
<M恒成立,若存在,求出M-m的最小值;若不存在,说明理由.(1) an=2n-1 (2) M-m的最小值为2.
(1)据题意:f(1)=n2 即
令n="1" 则a0+a1=1,a1=1-a0 令n="2" 则a0+a1+a2=22,a2=4-(a0+a1)=4-1=3
令n="3" 则a0+a1+a2+a3=32,a3=9-(a0+a1+a2)="9-4=5" ∵{an}为等差数列
∴d=a3-a2="5-3=2 " a1="3-2=1 " a0="0 " an=1+(n-1)·2=2n-1
(2)由(1)
n为奇数时,



相减得:

令 ,
,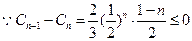
 .
.
∴Cn+1≤Cn,Cn随n增大而减小 又 随n增大而减小
随n增大而减小
∴g( )为n的增函数,当n=1时,g(
)为n的增函数,当n=1时,g( )=
)=
而
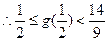
∴使m<g( )<M恒成立的自然m的最大值为0,M最小值为2. M-m的最小值为2.
)<M恒成立的自然m的最大值为0,M最小值为2. M-m的最小值为2.

令n="1" 则a0+a1=1,a1=1-a0 令n="2" 则a0+a1+a2=22,a2=4-(a0+a1)=4-1=3
令n="3" 则a0+a1+a2+a3=32,a3=9-(a0+a1+a2)="9-4=5" ∵{an}为等差数列
∴d=a3-a2="5-3=2 " a1="3-2=1 " a0="0 " an=1+(n-1)·2=2n-1
(2)由(1)

n为奇数时,




相减得:


令
 ,
,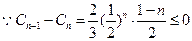
 .
.∴Cn+1≤Cn,Cn随n增大而减小 又
 随n增大而减小
随n增大而减小∴g(
 )为n的增函数,当n=1时,g(
)为n的增函数,当n=1时,g( )=
)=
而

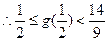
∴使m<g(
 )<M恒成立的自然m的最大值为0,M最小值为2. M-m的最小值为2.
)<M恒成立的自然m的最大值为0,M最小值为2. M-m的最小值为2.
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
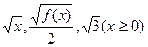 成等差数列.又数列
成等差数列.又数列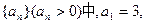 此数列的前n项的和Sn(
此数列的前n项的和Sn(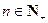 )对所有大于1的正整数n都有
)对所有大于1的正整数n都有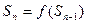 .(1)求数列
.(1)求数列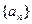 的第n+1项;(2)若
的第n+1项;(2)若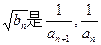 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn. 中,已知
中,已知 .
. 且
且 的前项
的前项 和为
和为 ,求证:
,求证: .
.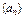 满足
满足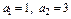 ,且
,且 。
。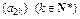 为等比数列;(2)求数列
为等比数列;(2)求数列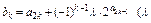 为非零常数)。试确定
为非零常数)。试确定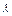 的值,使得对任意
的值,使得对任意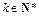 都有
都有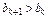 成立。
成立。 中,已知
中,已知 则
则 等于
等于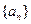 的前
的前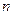 项和
项和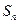 和通项
和通项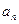 满足
满足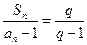 (
(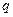 是常数且
是常数且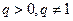 )。(Ⅰ)求数列
)。(Ⅰ)求数列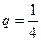 时,试证明
时,试证明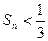 ;
;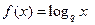 ,
,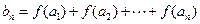 ,是否存在正整数
,是否存在正整数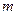 ,使
,使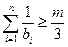 对
对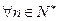 都成立?若存在,求出
都成立?若存在,求出 满足
满足 ,
, ,且
,且 ,
, ,
, 成等差数列,则
成等差数列,则 的值是( )
的值是( )