题目内容
(本小题满分14分)
已知曲线 .从点
.从点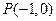 向曲线
向曲线 引斜率为
引斜率为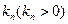 的切线
的切线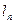 ,切点为
,切点为 。
。
(1)求数列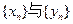 的通项公式;
的通项公式;
(2)证明: 。
。
已知曲线
 .从点
.从点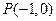 向曲线
向曲线 引斜率为
引斜率为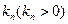 的切线
的切线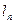 ,切点为
,切点为 。
。(1)求数列
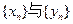 的通项公式;
的通项公式;(2)证明:
 。
。(1)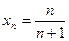 ;
;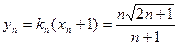
(2)证明见解析。
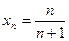 ;
;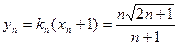
(2)证明见解析。
(1)设直线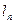 :
: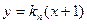 ,联立
,联立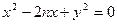 得:
得:
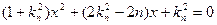 ,则
,则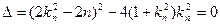 ,∴
,∴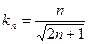 (
(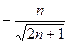 舍去)
舍去)
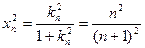 ,即
,即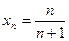 ,∴
,∴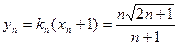
(2)证明:∵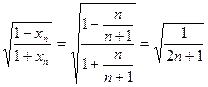
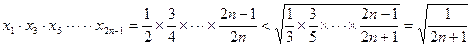
∴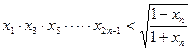
由于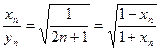 ,可令函数
,可令函数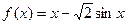 ,则
,则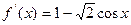 ,令
,令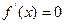 ,得
,得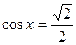 ,给定区间
,给定区间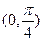 ,则有
,则有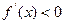 ,则函数
,则函数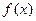 在
在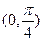 上单调递减,∴
上单调递减,∴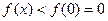 ,即
,即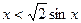 在
在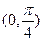 恒成立,又
恒成立,又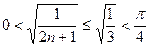 ,
,
则有 ,即
,即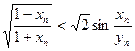
 。
。
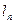 :
: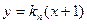 ,联立
,联立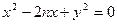 得:
得: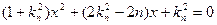 ,则
,则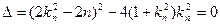 ,∴
,∴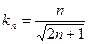 (
(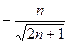 舍去)
舍去)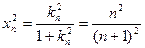 ,即
,即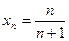 ,∴
,∴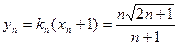
(2)证明:∵
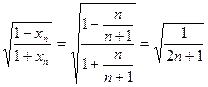
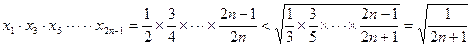
∴
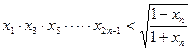
由于
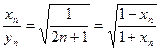 ,可令函数
,可令函数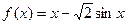 ,则
,则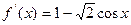 ,令
,令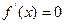 ,得
,得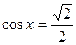 ,给定区间
,给定区间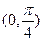 ,则有
,则有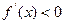 ,则函数
,则函数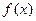 在
在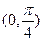 上单调递减,∴
上单调递减,∴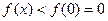 ,即
,即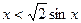 在
在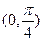 恒成立,又
恒成立,又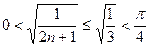 ,
,则有
 ,即
,即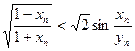
 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
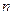 为正整数时,区间
为正整数时,区间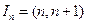 ,
,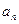 表示函数
表示函数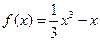 在
在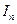 上函数值取整数值的个数,当
上函数值取整数值的个数,当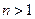 时,记
时,记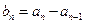 .当
.当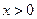 ,
,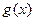 表示把
表示把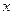 “四舍五入”到个位的近似值,如
“四舍五入”到个位的近似值,如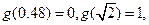
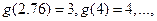 当
当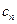 表示满足
表示满足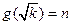 的正整数
的正整数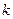 的个数.
的个数.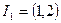 的单调性;
的单调性;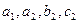 ;
;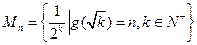 中所有元素之和为
中所有元素之和为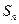 ,记
,记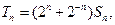 求证:
求证: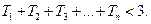
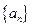 满足递推关系
满足递推关系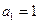 且
且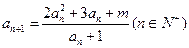 .
.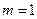 时,求数列
时,求数列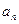 ;(2) 当
;(2) 当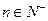 时,数列
时,数列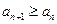 恒成立,求
恒成立,求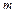 的取值范围;(3) 在
的取值范围;(3) 在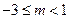 时,证明:
时,证明: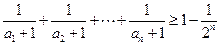 .
.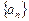 中,其中
中,其中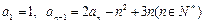
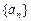 的通项公式;
的通项公式;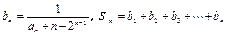 ,证明:当
,证明:当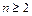 时,
时,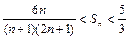 .
.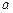 的值依次分别记为
的值依次分别记为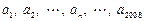 ,将输出的
,将输出的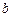 的值依次分别记为
的值依次分别记为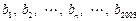 .
.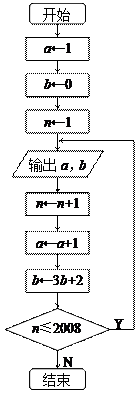
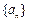 ,
,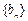 通项公式;
通项公式;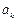 与
与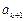 中插入
中插入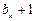 个3,就能得到一个新数列
个3,就能得到一个新数列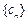 ,则
,则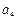 是数列
是数列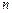 项和为
项和为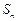 ,问是否存在这样的正整数
,问是否存在这样的正整数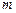 ,使数列
,使数列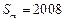 ,如果存在,求出
,如果存在,求出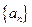 的前
的前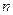 项和为
项和为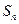 ,若
,若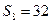 ,
,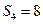 ,则它的首项与公差分别是( )
,则它的首项与公差分别是( )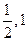
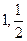
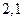
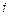 行第
行第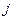 列的数为
列的数为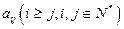 ,则
,则