题目内容
【题目】设等差数列{an}的公差为d，点（an ， bn）在函数f（x）=2x的图象上（n∈N*）．
（1）若a1=﹣2，点（a8 ， 4b7）在函数f（x）的图象上，求数列{an}的前n项和Sn；
（2）若a1=1，函数f（x）的图象在点（a2 ， b2）处的切线在x轴上的截距为2﹣ 
，求数列{ 
}的前n项和Tn ．
【答案】
（1）解：∵点（an，bn）在函数f（x）=2x的图象上，
∴ 
，
又等差数列{an}的公差为d，
∴ 
= 
=2d，
∵点（a8，4b7）在函数f（x）的图象上，
∴ 
=b8，
∴ 
=4=2d，解得d=2．
又a1=﹣2，∴Sn= 
=﹣2n+ 
=n2﹣3n
（2）解：由f（x）=2x，∴f′（x）=2xln2，
∴函数f（x）的图象在点（a2，b2）处的切线方程为 
，
又 
，令y=0可得x= 
，
∴ 
，解得a2=2．
∴d=a2﹣a1=2﹣1=1．
∴an=a1+（n﹣1）d=1+（n﹣1）×1=n，
∴bn=2n．
∴ 
．
∴Tn= 
+…+ 
+ 
，
∴2Tn=1+ 
+ 
+…+ 
，
两式相减得Tn=1+ 
+…+ 
﹣ = 
﹣
= 
= 
．
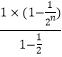【解析】（1）由于点（an ， bn）在函数f（x）=2x的图象上，可得 ，又等差数列{an}的公差为d，利用等差数列的通项公式可得 =2d ． 由于点（a8 ， 4b7）在函数f（x）的图象上，可得 =b8 ， 进而得到 =4=2d ， 解得d．再利用等差数列的前n项和公式即可得出．（2）利用导数的几何意义可得函数f（x）的图象在点（a2 ， b2）处的切线方程，即可解得a2 ． 进而得到an ， bn ． 再利用“错位相减法”即可得出．
【考点精析】掌握数列的前n项和是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系
．
