题目内容
【题目】若函数![]() 和
和![]() 满足:
满足:![]() 在区间
在区间![]() 上均有定义;
上均有定义;![]() 函数
函数![]() 在区间
在区间![]() 上至少有一个零点,则称
上至少有一个零点,则称![]() 和
和![]() 在
在![]() 上具有关系W.
上具有关系W.
![]() 若
若![]() ,
,![]() ,判断
,判断![]() 和
和![]() 在
在![]() 上是否具有关系W,并说明理由;
上是否具有关系W,并说明理由;
![]() 若
若![]() 和
和![]() 在
在![]() 上具有关系W,求实数m的取值范围.
上具有关系W,求实数m的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据[a,b]上至少有一个零点,则称f(x)和g(x)在区间[a,b]上具有关系G.利用特殊值但判断出即可;(2)根据在区间[a,b]上具有关系G的性质,结合x∈[1,4],利用二次函数的性质,讨论m即可.
(1)f(x)和g(x)在[1,3]具有关系G.
令h(x)=f(x)﹣g(x)=lnx+x﹣2,
∵h(1)=﹣1<0,h(2)=ln2>0;
故h(1)h(2)<0,又h(x)在[1,2]上连续,
故函数y=f(x)﹣g(x)在区间[1,2]上至少有一个零点,
故f(x)和g(x)在[1,3]上具有关系G;
(2)令h(x)=f(x)﹣g(x)=2|x﹣2|+1﹣mx2,
当m≤0时,易知h(x)在[1,4]上不存在零点,
当m>0时,h(x)=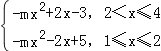 ,
,
当1≤x≤2时,
由二次函数知h(x)在[1,2]上单调递减,
故![]() ,
,
故m∈[![]() ,3],
,3],
当m∈(0,![]() )∪(3,+∞)时,
)∪(3,+∞)时,
若m∈(0,![]() ),则h(x)在(2,4]上单调递增,
),则h(x)在(2,4]上单调递增,
而h(2)>0,h(4)>0;
故没有零点;
若m∈(3,+∞),则h(x)在(2,4]上单调递减,
此时,h(2)=﹣4m+1<0;
故没有零点;
综上所述,
若f(x)=2|x﹣2|+1和g(x)=mx2在[1,4]上具有关系G,
则m∈[![]() ,3].
,3].

【题目】某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意程度进行调查,并随机抽取了其中30名员工(16名女工,14名男工)的得分,如下表:
女 | 47 | 36 | 32 | 48 | 34 | 44 | 43 | 47 | 46 | 41 | 43 | 42 | 50 | 43 | 35 | 49 |
男 | 37 | 35 | 34 | 43 | 46 | 36 | 38 | 40 | 39 | 32 | 48 | 33 | 40 | 34 |
(1)根据以上数据,估计该企业得分大于45分的员工人数;
(2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平局得分为 “满意”,否则为 “不满意”,请完成下列表格:
“满意”的人数 | “不满意”的人数 | 合计 | |
女员工 | 16 | ||
男员工 | 14 | ||
合计 | 30 |
(3)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关?
参考数据:
P(K2 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
K | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
![]()

