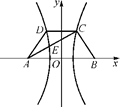
题目内容
如图,已知梯形ABCD中|AB|=2|CD|,点E满足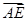 =λ
=λ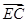 ,双曲线过C、D、E三点,且以A、B为焦点.当
,双曲线过C、D、E三点,且以A、B为焦点.当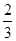 ≤λ≤
≤λ≤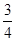 时,求双曲线离心率e的取值范围.
时,求双曲线离心率e的取值范围.
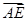 =λ
=λ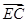 ,双曲线过C、D、E三点,且以A、B为焦点.当
,双曲线过C、D、E三点,且以A、B为焦点.当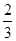 ≤λ≤
≤λ≤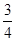 时,求双曲线离心率e的取值范围.
时,求双曲线离心率e的取值范围.
[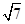 ,
,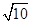 ].
].
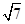 ,
,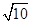 ].
].如题图,以直线AB为x轴,AB的垂直平分线为y轴,建立直角坐标系xOy,则CD⊥y轴.因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于y轴对称.根据已知,设A(-c,0),C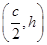 ,E(x0,y0),其中c=
,E(x0,y0),其中c=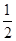 |AB|为双曲线的半焦距,h是梯形的高.由
|AB|为双曲线的半焦距,h是梯形的高.由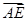 =λ
=λ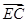 ,即(x0+c,y0)=λ
,即(x0+c,y0)=λ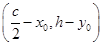 ,得
,得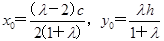 .不妨设双曲线的方程为
.不妨设双曲线的方程为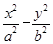 =1,则离心率e=
=1,则离心率e=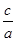 .由点C、E在双曲线上,将点C、E的坐标和e=
.由点C、E在双曲线上,将点C、E的坐标和e=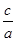 代入双曲线的方程得
代入双曲线的方程得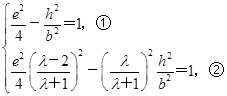
由①式得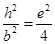 -1,③
-1,③
将③式代入②式,整理得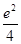 (4-4λ)=1+2λ,所以λ=1-
(4-4λ)=1+2λ,所以λ=1-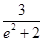 .由已知
.由已知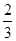 ≤λ≤
≤λ≤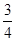 ,所以
,所以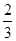 ≤1-
≤1-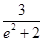 ≤
≤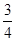 ,解之得
,解之得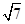 ≤e≤
≤e≤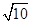 ,所以双曲线的离心率的取值范围为[
,所以双曲线的离心率的取值范围为[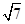 ,
,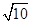 ].
].
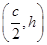 ,E(x0,y0),其中c=
,E(x0,y0),其中c=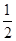 |AB|为双曲线的半焦距,h是梯形的高.由
|AB|为双曲线的半焦距,h是梯形的高.由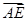 =λ
=λ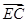 ,即(x0+c,y0)=λ
,即(x0+c,y0)=λ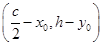 ,得
,得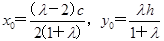 .不妨设双曲线的方程为
.不妨设双曲线的方程为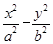 =1,则离心率e=
=1,则离心率e=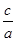 .由点C、E在双曲线上,将点C、E的坐标和e=
.由点C、E在双曲线上,将点C、E的坐标和e=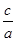 代入双曲线的方程得
代入双曲线的方程得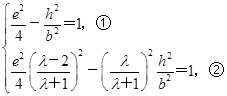
由①式得
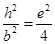 -1,③
-1,③将③式代入②式,整理得
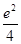 (4-4λ)=1+2λ,所以λ=1-
(4-4λ)=1+2λ,所以λ=1-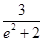 .由已知
.由已知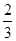 ≤λ≤
≤λ≤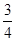 ,所以
,所以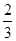 ≤1-
≤1-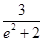 ≤
≤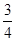 ,解之得
,解之得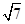 ≤e≤
≤e≤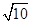 ,所以双曲线的离心率的取值范围为[
,所以双曲线的离心率的取值范围为[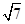 ,
,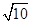 ].
].
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的内切圆与三边
的内切圆与三边 的切点分别为
的切点分别为 ,已知
,已知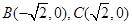 ,内切圆圆心
,内切圆圆心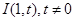 ,设点A的轨迹为R.
,设点A的轨迹为R. 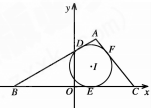
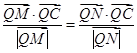 恒成立,若求出Q点的坐标,若不存在,说明理由.
恒成立,若求出Q点的坐标,若不存在,说明理由.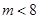 ”是“方程
”是“方程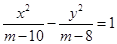 表示双曲线”的( )
表示双曲线”的( )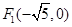 ,点P在双曲线上,且线段
,点P在双曲线上,且线段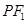 的中点坐标为(0,2),则此双曲线的方程是________________.
的中点坐标为(0,2),则此双曲线的方程是________________. 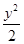 =1,过定点P(2,1)作直线交双曲线于P1、P2两点,并使P(2,1)为P1P2的中点,则此直线方程是____________.
=1,过定点P(2,1)作直线交双曲线于P1、P2两点,并使P(2,1)为P1P2的中点,则此直线方程是____________.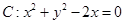 的圆心到双曲线
的圆心到双曲线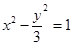 的渐近线的距离是( )
的渐近线的距离是( )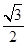
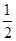
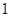
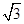
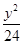 =1的两个焦点,P是双曲线上的一点,且3PF1=4PF2,则△PF1F2的面积等于________.
=1的两个焦点,P是双曲线上的一点,且3PF1=4PF2,则△PF1F2的面积等于________.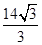 ,且∠ABC=120°,BC=10,边BC在x轴上且y轴垂直平分BC边,则过点A且以B,C为焦点的双曲线方程为( )
,且∠ABC=120°,BC=10,边BC在x轴上且y轴垂直平分BC边,则过点A且以B,C为焦点的双曲线方程为( )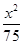 -
-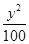 =1
=1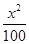 -
-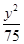 =1
=1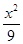 -
-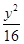 =1
=1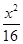 -
-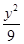 =1
=1