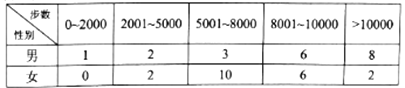
题目内容
【题目】用数学归纳法证明
，则当n=k+1时左端应在n=k的基础上加上（ ）
A.（3k+2）
B.（3k+4）
C.（3k+2）+（3k+3）
D.（3k+2）+（3k+3）+（3k+4）
【答案】D
【解析】当n=k时，等式左端=1+2+…+（3k+1），
当n=k+1时，等式左端=1+2+…+（3k+1）+（3k+2）+（3k+3）+（3k+4），
即当n=k+1时左端应在n=k的基础上加上（3k+1）+（3k+2）+（3k+3）+（3k+4）．
故选：D．
【考点精析】本题主要考查了数学归纳法的步骤的相关知识点，需要掌握
- 步骤:A.命题在n=1（或
）时成立，这是递推的基础；B.假设在n=k时命题成立； C.证明n=k+1时命题也成立,完成这两步,就可以断定对任何自然数(或n>=,且
)结论都成立
才能正确解答此题．
练习册系列答案
相关题目
