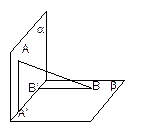题目内容
(本小题满分12分)直三棱柱ABC -A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.
(Ⅰ)求证:AC⊥B1C;
(Ⅱ)若D是AB中点,求证:AC1∥平面B1CD;
(Ⅲ)当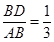
 时,求二面角
时,求二面角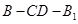 的余弦值.
的余弦值.
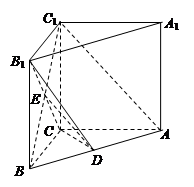
(Ⅰ)求证:AC⊥B1C;
(Ⅱ)若D是AB中点,求证:AC1∥平面B1CD;
(Ⅲ)当
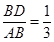
 时,求二面角
时,求二面角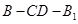 的余弦值.
的余弦值.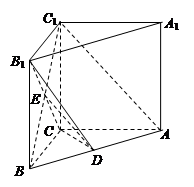
18.(Ⅰ)证明:在△ABC中,因为 AB=5,AC=4,BC=3,
所以AC2+ BC2= AB2, 所以 AC⊥BC.
因为直三棱柱ABC-A1B1C1,所以C C1⊥AC.
因为BC∩AC =C, 所以 AC⊥平面B B1C1C.
所以 AC⊥平面B B1C1C.
所以AC⊥B1C. …………4分
(Ⅱ)证明:连结BC1,交B1C于E,连接DE.
因为直三棱柱ABC-A1B1C1,D是AB中点,所以侧面B B1C1C为矩形,DE为△ABC1的中位线,
所以DE// AC1.因为DE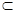 平面B1CD, AC1
平面B1CD, AC1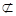 平面B1CD,所以AC1∥平面B1CD.........8分
平面B1CD,所以AC1∥平面B1CD.........8分

(Ⅲ)解:由(Ⅰ)知AC⊥BC,如图,以C为原点建立空间直角坐标系C-xyz.则B (3, 0, 0),A (0, 4, 0),A1(0, 4, 4),B1(3, 0, 4).
设D (a, b, 0)(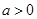 ,
, ),
),
因为点D在线段AB上,且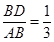 ,即
,即 .
.
所以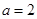 ,
,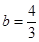 ,
,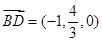 ,
,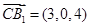 , ,
, , .
.
平面BCD的法向量为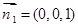 .设平面B1 CD的法向量为
.设平面B1 CD的法向量为 ,
,
由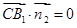 ,
,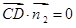 ,得
,得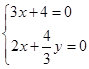 ,
,
所以 ,
,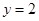 ,
, .所以
.所以 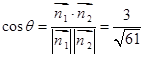 .
.
所以二面角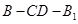 的余弦值为
的余弦值为 .……………12分
.……………12分
所以AC2+ BC2= AB2, 所以 AC⊥BC.
因为直三棱柱ABC-A1B1C1,所以C C1⊥AC.
因为BC∩AC =C,
 所以 AC⊥平面B B1C1C.
所以 AC⊥平面B B1C1C. 所以AC⊥B1C. …………4分
(Ⅱ)证明:连结BC1,交B1C于E,连接DE.
因为直三棱柱ABC-A1B1C1,D是AB中点,所以侧面B B1C1C为矩形,DE为△ABC1的中位线,
所以DE// AC1.因为DE
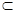 平面B1CD, AC1
平面B1CD, AC1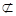 平面B1CD,所以AC1∥平面B1CD.........8分
平面B1CD,所以AC1∥平面B1CD.........8分
(Ⅲ)解:由(Ⅰ)知AC⊥BC,如图,以C为原点建立空间直角坐标系C-xyz.则B (3, 0, 0),A (0, 4, 0),A1(0, 4, 4),B1(3, 0, 4).
设D (a, b, 0)(
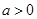 ,
, ),
),因为点D在线段AB上,且
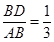 ,即
,即 .
.所以
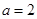 ,
,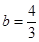 ,
,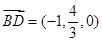 ,
,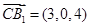 , ,
, , .
.平面BCD的法向量为
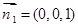 .设平面B1 CD的法向量为
.设平面B1 CD的法向量为 ,
,由
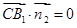 ,
,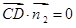 ,得
,得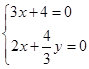 ,
,所以
 ,
,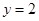 ,
, .所以
.所以 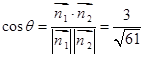 .
.所以二面角
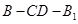 的余弦值为
的余弦值为 .……………12分
.……………12分略

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
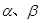 是两个不同的平面,m、n是平面
是两个不同的平面,m、n是平面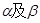 之外的两条不同的直线,给出四个论断: ①m⊥n,②
之外的两条不同的直线,给出四个论断: ①m⊥n,②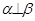 ,③
,③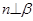 ,④
,④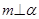 。
。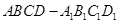 中,底面
中,底面 是边长为
是边长为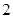 的正方形,
的正方形,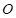 为
为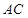 与
与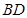 的交点,
的交点,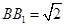 ,
,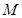 是线段
是线段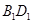 的中点.请建立空间直角坐标系解决以下问题:
的中点.请建立空间直角坐标系解决以下问题: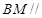 平面
平面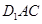 ;
;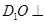 平面
平面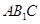 ;
;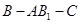 的大小.
的大小.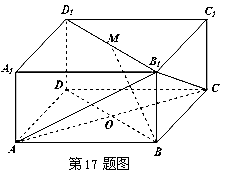
 所在的平面垂直于平面
所在的平面垂直于平面
 的中点为
的中点为 ,求证
,求证 ∥面
∥面
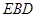 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值
的余弦值
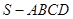 中,
中,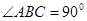 ,
,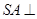 面
面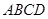 ,
, ,
,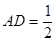 。
。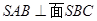 ;
;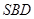 的距离。
的距离。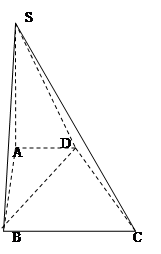
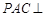 平面
平面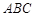 ,
, 是正三角形,
是正三角形,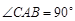 ,
,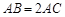 .
. 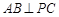 ;
; 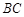 与平面
与平面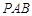 所成角的正弦值.
所成角的正弦值.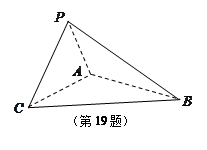

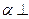 平面
平面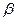 ,
,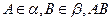 与两平面
与两平面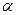 、
、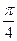 和
和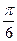 。过A、B分别作两平面交线的垂线,垂足为
。过A、B分别作两平面交线的垂线,垂足为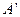 、
、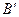 ,若AB=12,则
,若AB=12,则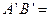 ( )
( )