题目内容
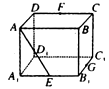
如图,已知直角梯形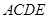 所在的平面垂直于平面
所在的平面垂直于平面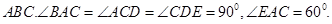
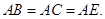
(1) 的中点为
的中点为 ,求证
,求证 ∥面
∥面
(2)求平面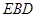 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值
的余弦值

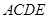 所在的平面垂直于平面
所在的平面垂直于平面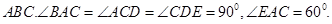
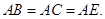
(1)
 的中点为
的中点为 ,求证
,求证 ∥面
∥面
(2)求平面
 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值
的余弦值
(1)在直角梯形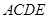 中,
中,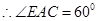 ,
,
 ∥
∥ 且
且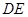 =
=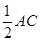 ………………………………(2分)
………………………………(2分)
设 的中点为
的中点为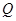 ,连结
,连结 ,
,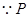 是
是 的中点
的中点
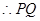 ∥
∥ 且
且 =
=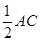 从而
从而 ∥
∥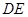 且
且 =
=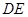 ……………………(4分)
……………………(4分)
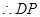 ∥
∥
 ∥面
∥面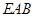 ……………………(6分)
……………………(6分)
(2)(法一)以 为坐标原点,
为坐标原点,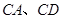 分别为
分别为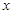 轴、
轴、 轴方向建立空间直角坐标系,分别求出平面
轴方向建立空间直角坐标系,分别求出平面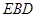 与平面
与平面 的法向量
的法向量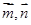 ,利用
,利用 与
与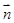 夹角的余弦值,来确定锐二面角
夹角的余弦值,来确定锐二面角 的余弦值,可得
的余弦值,可得 ……………………(12分)
……………………(12分)
(法二)不难证明,平面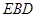 与平面
与平面 的交线平行于
的交线平行于 ,因此分别过
,因此分别过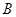 与
与 作
作 与
与 的平行线,两线交于
的平行线,两线交于
 面
面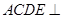 面
面

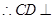 面
面
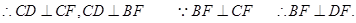
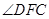 是平面
是平面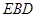 与平面
与平面 所成锐二面角的平面角.
所成锐二面角的平面角.
设 ,则
,则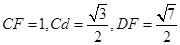
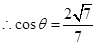
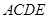 中,
中,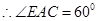 ,
,
 ∥
∥ 且
且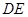 =
=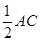 ………………………………(2分)
………………………………(2分)设
 的中点为
的中点为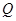 ,连结
,连结 ,
,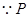 是
是 的中点
的中点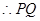 ∥
∥ 且
且 =
=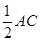 从而
从而 ∥
∥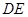 且
且 =
=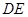 ……………………(4分)
……………………(4分)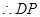 ∥
∥
 ∥面
∥面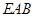 ……………………(6分)
……………………(6分)(2)(法一)以
 为坐标原点,
为坐标原点,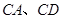 分别为
分别为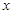 轴、
轴、 轴方向建立空间直角坐标系,分别求出平面
轴方向建立空间直角坐标系,分别求出平面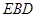 与平面
与平面 的法向量
的法向量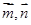 ,利用
,利用 与
与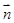 夹角的余弦值,来确定锐二面角
夹角的余弦值,来确定锐二面角 的余弦值,可得
的余弦值,可得 ……………………(12分)
……………………(12分)(法二)不难证明,平面
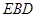 与平面
与平面 的交线平行于
的交线平行于 ,因此分别过
,因此分别过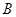 与
与 作
作 与
与 的平行线,两线交于
的平行线,两线交于
 面
面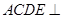 面
面

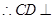 面
面
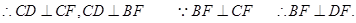
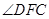 是平面
是平面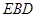 与平面
与平面 所成锐二面角的平面角.
所成锐二面角的平面角.设
 ,则
,则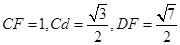
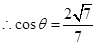
略

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
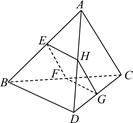
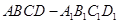 中,E,P分别是侧棱B1C1,
中,E,P分别是侧棱B1C1,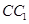 上的中点
上的中点 所成角的正切值
所成角的正切值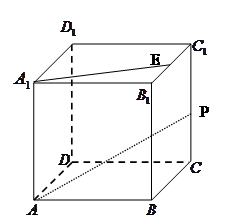
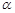 的一个充分条件是( )
的一个充分条件是( )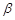 ,
,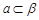 ,
,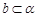 ,a∥b
,a∥b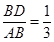
 时,求二面角
时,求二面角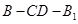 的余弦值.
的余弦值.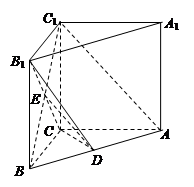
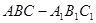 中,
中,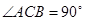 ,
,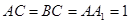 ,
,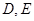 分别为棱
分别为棱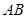 、
、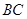 的中点,
的中点,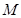 为棱
为棱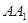 上的点。
上的点。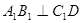 ;
;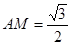 时,求二面角
时,求二面角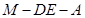 的大小。
的大小。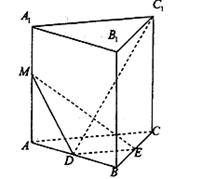
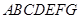 中,平面
中,平面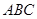 ∥平面
∥平面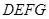 ,
,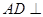 平面
平面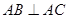 ,
, ,
,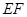 ∥
∥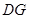 ,且
,且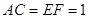 ,
,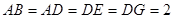 .
.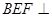 平面
平面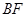 ∥平面
∥平面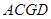 ;
;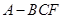 的体积.
的体积.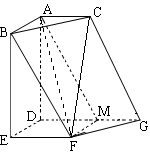
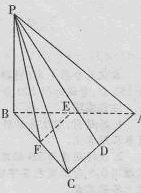
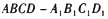 中,E,F,G分别是
中,E,F,G分别是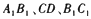 的中点,则下列中与直线AE有关的正确命题是
的中点,则下列中与直线AE有关的正确命题是