题目内容
已知函数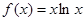 ,
,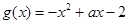
(1)求函数 在
在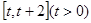 上的最小值;
上的最小值;
(2)若函数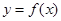 与
与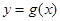 的图像恰有一个公共点,求实数a的值;
的图像恰有一个公共点,求实数a的值;
(3)若函数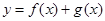 有两个不同的极值点
有两个不同的极值点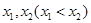 ,且
,且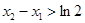 ,求实数a的取值范围。
,求实数a的取值范围。
(1)当 时最小值
时最小值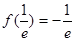 ,当
,当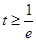 时最小值
时最小值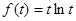 (2)3(3)
(2)3(3)
解析试题分析:(1)令 ,得
,得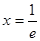 ,①当
,①当 时,函数
时,函数 在
在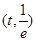 上单调递减,在
上单调递减,在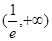 上单调递增。此时最小值为
上单调递增。此时最小值为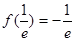 ;②当
;②当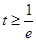 时,函数在
时,函数在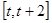 上单调递增,此时最小值为
上单调递增,此时最小值为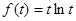 。
。
(2)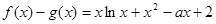 在
在 上有且仅有仅有一个根,即
上有且仅有仅有一个根,即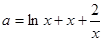 在
在 上有且仅有仅有一个根,令
上有且仅有仅有一个根,令 ,则
,则 ,
,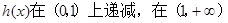 上递增,所以
上递增,所以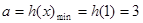 。
。
(3)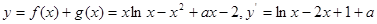 ,由题意知
,由题意知 有两个不同的实数根
有两个不同的实数根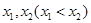 ,等价于
,等价于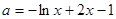 有两个不同的实数根
有两个不同的实数根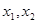 ,等价于直线
,等价于直线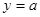 与函数
与函数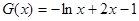 的图像有两个不同的交点。
的图像有两个不同的交点。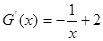 ,
,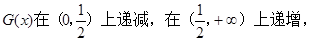 所以当
所以当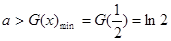 时,
时,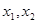 存在,且
存在,且 的值随着
的值随着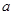 的增大而增大。
的增大而增大。
而当 时,则有
时,则有 ,两式相减得
,两式相减得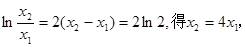 代入
代入 ,解得
,解得 此时
此时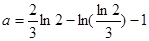 ,所以实数
,所以实数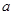 的取值范围为
的取值范围为
考点:函数单调性最值
点评:第一小题求最值需对参数分情况讨论从而确定最值点的位置,第二小题将方程的根的情况转化为函数最值得判定,这种转化方法包括将不等式恒成立问题转化为函数最值问题都是函数题目中经常用到的思路,须加以重视

练习册系列答案
相关题目
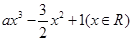 ,其中a>0,
,其中a>0, 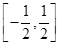 上,f(x)>0恒成立,求a的取值范围。
上,f(x)>0恒成立,求a的取值范围。 ,
,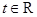 .
.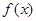 的极值点;
的极值点; 对
对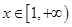 恒成立,求实数
恒成立,求实数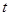 的取值范围.
的取值范围. .
. 时,求证:函数
时,求证:函数 在
在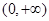 上单调递增;
上单调递增;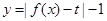 有三个零点,求
有三个零点,求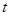 的值.
的值.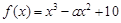 ,
,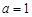 时,求曲线
时,求曲线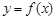 在点
在点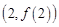 处的切线方程;
处的切线方程;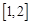 内至少存在一个实数
内至少存在一个实数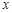 ,使得
,使得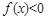 成立,求实数
成立,求实数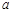 的取值范围.
的取值范围.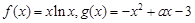 .
.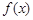 在
在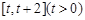 上的最小值;
上的最小值;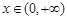 ,
,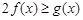 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.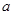 为实数,
为实数,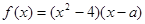
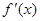 ;
;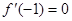 ,求
,求 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;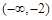 和
和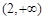 上都是递增的,求
上都是递增的,求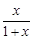 .
.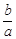 .
. ,
, ,
, 所围成的平面图形的面积。
所围成的平面图形的面积。