题目内容
已知函数f(x)=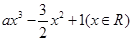 ,其中a>0,
,其中a>0,
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间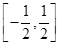 上,f(x)>0恒成立,求a的取值范围。
上,f(x)>0恒成立,求a的取值范围。
(Ⅰ)y=6x-9;(Ⅱ)a的范围为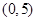 。
。
解析试题分析:(Ⅰ)解:当a=1时,f(x)=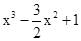 ,f(2)=3;
,f(2)=3;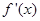 =
=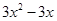 ,
, 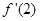 =6.
=6.
所以曲线y=f(x)在点(2,f(2))处的切线方程为y-3=6(x-2),即y=6x-9
(Ⅱ)解: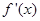 =
=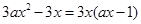 .令f’(x)=0,解得x=0或x=
.令f’(x)=0,解得x=0或x=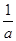 . 5分
. 5分
以下分两种情况讨论:
(1)若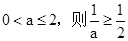 ,当x变化时,
,当x变化时,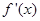 ,f(x)的变化情况如表:
,f(x)的变化情况如表:
当x 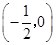
0 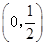
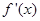
+ 0 - f(x) 
极大值 
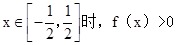 等价于
等价于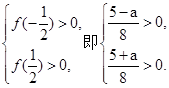
解不等式组得-5<a<5.因此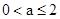 .
.
若a>2,则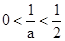 .当x变化时,
.当x变化时,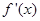 , f(x)的变化情况如下表:
, f(x)的变化情况如下表:x 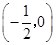
0 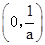
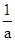
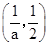
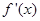
+ 0 -  练习册系列答案
练习册系列答案
学习与评价接力出版社系列答案
新课程学习与评价系列答案



快乐练练吧云南科技出版社系列答案

口算心算速算巧算系列答案
口算心算速算天天练习簿系列答案
新课程学习与测评高中版系列答案
相关题目
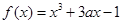 ,
,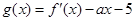 ,其中
,其中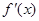 是
是 的导函数.
的导函数.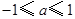 的一切
的一切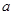 的值,都有
的值,都有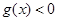 ,求实数
,求实数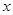 的取值范围;
的取值范围;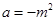 ,当实数
,当实数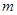 在什么范围内变化时,函数
在什么范围内变化时,函数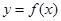 的图象与直线
的图象与直线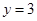 只有一个公共点.
只有一个公共点.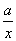 .
.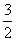 ,求a的值;
,求a的值;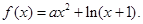
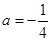 时,求函数
时,求函数 的单调区间;
的单调区间;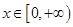 ,
,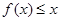 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.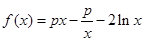 .
.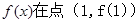 处的切线方程;
处的切线方程;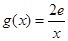 ,若在[1,e]上至少存在一点
,若在[1,e]上至少存在一点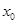 ,使得
,使得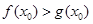 成立,求实
成立,求实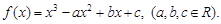 .
.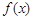 在
在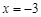 和
和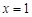 处取得极值,试求
处取得极值,试求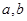 的值;
的值;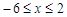 时,
时,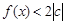 恒成立,求c的取值范围.
恒成立,求c的取值范围.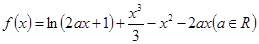
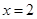 为
为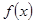 的极值点,求实数
的极值点,求实数 的值;
的值;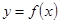 在
在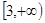 上为增函数,求实数
上为增函数,求实数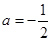 时,方程
时,方程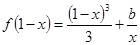 有实根,求实数
有实根,求实数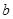 的最大值。
的最大值。 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数. 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.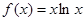 ,
,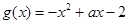
 在
在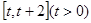 上的最小值;
上的最小值;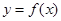 与
与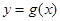 的图像恰有一个公共点,求实数a的值;
的图像恰有一个公共点,求实数a的值;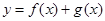 有两个不同的极值点
有两个不同的极值点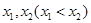 ,且
,且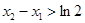 ,求实数a的取值范围。
,求实数a的取值范围。