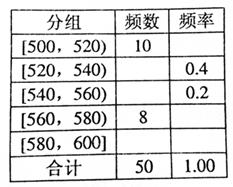
题目内容
某中学一位高三班主任对本班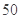 名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
| | 积极参加班级工作 | 不太主动参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太积极参加班级工作且学习积极性一般的学生的概率是多少?
(2)学生的积极性与对待班级工作的态度是否有关系?说明理由.
(1)
解析试题分析:(1)本题是一个古典概型,试验发生包含的事件数50,满足条件的事件数分别是24,19,根据概率公式得到结果.
(2)根据列联表所给的数据,代入求观测值的公式,求出观测值,把观测值同临界值进行比较,得到有99.9%的把握认为“学生的学习积极性与对待班级工作的态度”有关系.
(1)设“抽到积极参加班级工作的学生”为事件A,“抽到不太积极参加班级工作且学习积极性一般的学生”为事件B,则由古典概型
(2)根据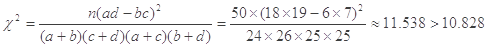
所以,我们有99.9%的把握认为“学生的学习积极性与对待班级工作的态度”有关系.
考点:古典概型,相关性分析

练习册系列答案
相关题目
假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
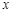 | 2 | 3 | 4 | 5 | 6 |
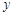 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示.已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16.
| | 第一批次 | 第二批次 | 第三批次 |
| 女教职工 | 196 | x | y |
| 男教职工 | 204 | 156 | z |
(1)求x的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查,问应在第三批次中抽取教职工多少名?
某普通高中共有教师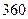 人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
| | 第一批次 | 第二批次 | 第三批次 |
| 女教师 | 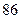 |  |  |
| 男教师 | 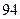 | 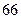 |  |
已知在全体教师中随机抽取1名,抽到第二、三批次中女教师的概率分别是
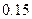 、
、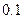 .
.(1)求
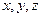 的值;
的值;(2)为了调查研修效果,现从三个批次中按
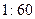 的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?(3)若从(2)中选取的教师中随机选出两名教师进行访谈,求参加访谈的两名教师“分别来自两个批次”的概率.
某种产品的广告费支出x与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
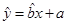 .
.(3)经计算,相关指数
 ,你可得到什么结论?
,你可得到什么结论?(参考数值:2×30+4×40+5×50+6×60+8×70==1390)


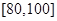 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份试卷的分数在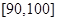 之间的概率;
之间的概率; 元/张
元/张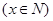 ,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少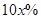 ,“铁杆足球迷”愿意前往观看的人数会减少
,“铁杆足球迷”愿意前往观看的人数会减少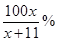 .问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
.问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?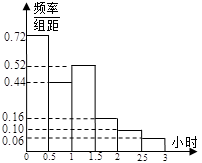

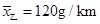 .
.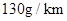 的概率是多少?
的概率是多少? 的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.
的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性.