题目内容
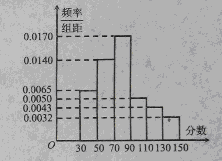
某校高一年级60名学生参加数学竞赛，成绩全部在40分至100分之间，现将成绩分成以下6段：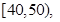
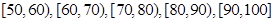，据此绘制了如图所示的频率分布直方图.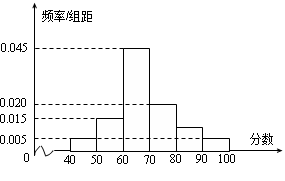 
（1）求成绩在区间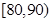
的频率；
（2）从成绩大于等于80分的学生中随机选3名学生，其中成绩在[90，100]内的学生人数为ξ，求ξ的分布列与均值.
（1）
；（2）分布列详见解析，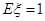
.
解析试题分析：本题主要考查频率分步直方图和离散型随机变量的分布列和数学期望等数学知识，考查学生的读图能力、分析问题和解决问题的能力、计算能力.第一问，利用频率分布直方图可知，所有频率之和为1，所有可以求出成绩在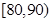的频率；第二问，通过频率分布直方图分别求出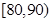和
内的学生人数，先列出
的可能取值，再分别求出每一种情况下的概率列出分布列，利用
求数学期望.
试题解析：（1）因为各组的频率之和为1，所以成绩在区间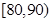的频率为
， 3分
（2）由已知和（1）的结果可知成绩在区间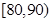内的学生有
人，
成绩在区间内的学生有
人， 4 分
依题意，ξ可能取的值为0，1，2，3 5 分
所以ξ的分布列为ξ 0 1 2 3 P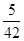 
10分
则均值Eξ=
12分
考点：1.频率分布直方图；2.离散型随机变量的分布列和数学期望.
阶梯计算系列答案某种产品的广告费支出x与销售额
(单位：百万元)之间有如下对应数据：
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
（1）请画出上表数据的散点图.
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
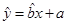.（3）经计算，相关指数
，你可得到什么结论？(参考数值：2×30+4×40+5×50+6×60+8×70==1390)
，求甲在初赛中答题个数
的分布列及数学期望
.一个车间为了规定工时定额．需要确定加工零件所花费的时间，为此进行了10次试验．测得的数据如下：
| 零件数x/个 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间y/分 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(2)如果y与x具有线性相关关系，求回归直线方程；
(3)根据求出的回归直线方程，预测加工200个零件所用的时间为多少？
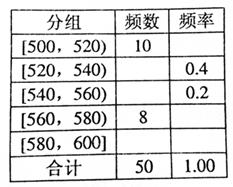
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示：
| | 积极参加班级工作 | 不太主动参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(2)试运用独立性检验的思想方法点拨：学生的学习积极性与对待班级工作的态度是否有关系？并说明理由.(参考下表)
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某单位N名员工参加“社区低碳你我他”活动，他们的年龄在25岁至50岁之间。按年龄分组：第1组
，第2组
，第3组
，第4组
，第5组
，由统计的数据得到的频率分布直方图如图所示，下表是年龄的频率分布表。
| 区间 | | | | | |
| 人数 |  | a | b | | |
（2）现要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，则年龄在第1，2，3组中抽取的人数分别是多少？
（3）在（2）的条件下，从这6人中随机抽取2人参加社区宣传交流活动，求恰有1 人在第3组的概率。
