题目内容
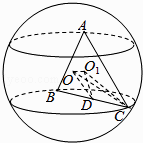
【题目】已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是 .
【答案】![]()
【解析】解:设正△ABC的中心为O1 , 连结O1O、O1C、O1E、OE, ∵O1是正△ABC的中心,A、B、C三点都在球面上,
∴O1O⊥平面ABC,结合O1C平面ABC,可得O1O⊥O1C,
∵球的半径R=2,球心O到平面ABC的距离为1,得O1O=1,
∴Rt△O1OC中,O1C= ![]() =
= ![]() .
.
又∵E为AB的中点,∴正△ABC中,O1E= ![]() O1C=
O1C= ![]() .
.
∴Rt△OO1E中,OE= ![]() =
= ![]() =
= ![]() .
.
∵过E作球O的截面,当截面与OE垂直时,截面圆的半径最小,
∴当截面与OE垂直时,截面圆的面积有最小值.
此时截面圆的半径r= ![]() =
= ![]() =
= ![]() ,
,
可得截面面积为S=πr2= ![]() .
.
所以答案是: ![]() .
.

练习册系列答案
相关题目


