题目内容
【题目】已知右焦点为F的椭圆C: ![]() +
+ ![]() =1(a>b>0)过点M(1,
=1(a>b>0)过点M(1, ![]() ),直线x=a与抛物线L:x2=
),直线x=a与抛物线L:x2= ![]() y交于点N,且
y交于点N,且 ![]() =
= ![]() ,其中O为坐标原点.
,其中O为坐标原点.
(1)求椭圆C的方程;
(2)直线l与椭圆C交于A、B两点.
①若直线l与x轴垂直,过点P(4,0)的直线PB交椭圆C于另一点E,证明直线AE与x轴相交于定点;
②已知D为椭圆C的左顶点,若l与直线DM平行,判断直线MA,MB是否关于直线FM对称,并说明理由.
【答案】
(1)解:设N(a,y0),连接MN,由 ![]() =
= ![]() ,则OMNF为平行四边形,则y0=
,则OMNF为平行四边形,则y0= ![]() ,
,
将M(1, ![]() )代入抛物线方程:解得:a=2,
)代入抛物线方程:解得:a=2,
将M(1, ![]() )代入椭圆方程:
)代入椭圆方程: ![]() ,解得:b2=3,
,解得:b2=3,
∴椭圆的标准方程: ![]()
(2)解:①证明:由题意,直线PB的斜率存在,设直线PB的方程为y=k(x﹣4),B(x1,y1),E(x2,y2),
则A(x1,﹣y1), ![]() ,整理得:(3+4k2)x2﹣32k2x+64k2﹣12=0,
,整理得:(3+4k2)x2﹣32k2x+64k2﹣12=0,
x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,①
,①
则直线AE的方程为:y﹣y2= ![]() (x﹣x2),令y=0,x=x2﹣
(x﹣x2),令y=0,x=x2﹣ ![]() ,
,
由y1=k(x1﹣4),y2=k(x2﹣4),
∴x= ![]() ,
,
∴x=1,
∴直线AE与x轴相交于定点(1,0);
②由题意可知,直线MF的方程为x=1,则kOM= ![]() ,设直线l:y=
,设直线l:y= ![]() x+n,(n≠1),
x+n,(n≠1),
设A(x3,y3),B(x4,y4), 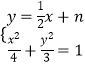 ,整理得:x2+nx+n2﹣3=0,
,整理得:x2+nx+n2﹣3=0,
△=n2﹣4×(n2﹣3)=12﹣3n2>0,即b∈(﹣2,2),且n≠1,
x3+x4=﹣n,x3x4=n2﹣3,
则kMA+kMB= ![]() +
+ ![]() =
= ![]() +
+ ![]()
=1+ ![]() +
+ ![]() =1+
=1+ ![]() =1﹣
=1﹣ ![]() =0,
=0,
直线MA,MB关于直线x=1对称
【解析】(1)将由 ![]() =
= ![]() ,即可求得N点坐标,将M代入抛物线方程,即可求得a,代入椭圆方程,即可求得b的值,即可求得椭圆方程;(2)①设直线PB的方程,设B,E点坐标,将直线PB代入椭圆方程,求得直线AE的方程,利用韦达定理即可求得x的值,直线AE与x轴相交于定点(1,0);
,即可求得N点坐标,将M代入抛物线方程,即可求得a,代入椭圆方程,即可求得b的值,即可求得椭圆方程;(2)①设直线PB的方程,设B,E点坐标,将直线PB代入椭圆方程,求得直线AE的方程,利用韦达定理即可求得x的值,直线AE与x轴相交于定点(1,0);
②设直线l的方程,代入椭圆方程,由△>0,即可求得n的取值范围,利用直线的斜率公式及韦达定理kMA+kMB=0,则直线MA,MB关于直线x=1对称.

【题目】某科技公司生产一种手机加密芯片,其质量按测试指标划分为:指标大于或等于70为合格品,小于70为次品.现随机抽取这种芯片共120件进行检测,检测结果统计如表:
测试指标 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
芯片数量(件) | 8 | 22 | 45 | 37 | 8 |
已知生产一件芯片,若是合格品可盈利400元,若是次品则亏损50元.
(Ⅰ)试估计生产一件芯片为合格品的概率;并求生产3件芯片所获得的利润不少于700元的概率.
(Ⅱ)记ξ为生产4件芯片所得的总利润,求随机变量ξ的分布列和数学期望.
