题目内容
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为元.
【答案】216000
【解析】解:设A、B两种产品分别是x件和y件,获利为z元.
由题意,得 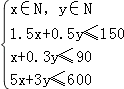 ,z=2100x+900y.
,z=2100x+900y.
不等式组表示的可行域如图:由题意可得 ![]() ,解得:
,解得: ![]() ,A(60,100),
,A(60,100),
目标函数z=2100x+900y.经过A时,直线的截距最大,目标函数取得最大值:2100×60+900×100=216000元.
故答案为:216000.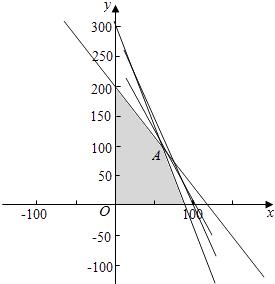
设A、B两种产品分别是x件和y件,根据题干的等量关系建立不等式组以及目标函数,利用线性规划作出可行域,通过目标函数的几何意义,求出其最大值即可;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

