题目内容
【题目】已知函数f(x)=xlnx﹣ ![]() x2﹣x+a(a∈R).
x2﹣x+a(a∈R).
(1)当a=0时,求f(x)的单调区间;
(2)若函数f(x)在其定义域内有两个不同的极值点.
(ⅰ)求a的取值范围;
(ⅱ)设两个极值点分别为x1 , x2 , 证明:x1x2>e2 .
【答案】
(1)解:当a=0时,f(x)=xlnx﹣x.
函数f(x)的定义域为x>0,f'(x)=lnx;
当x>1时,f'(x)>0;当0<x<1时,f'(x)<0.
所以,f(x)在(0,1)上单调递减;在(1,+∞)上单调递增.
(2)解:(ⅰ)依题意,函数f(x)的定义域为x>0,f'(x)=lnx﹣ax
所以方程f'(x)=0在x>0上有两个不同根,即:
方程lnx﹣ax=0在x>0上有两个不同根,转化为:函数y=lnx与函数y=ax
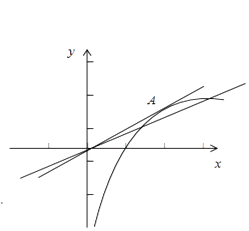
的图象在x>0上有两个不同交点,如图.
可见,若令过原点且切于函数y=lnx图象的直线斜率为k,只须0<a<k.
令切点A(x0,lnx0),所以k= ![]() ,又k=
,又k= ![]() ,所以
,所以 ![]() ,
,
解得:x0=e,于是k= ![]() ,
,
所以,0<a< ![]() .
.
(ⅱ)由(i)可知x1,x2分别是方程lnx﹣ax=0的两个根,
即lnx1=ax1,lnx2=ax2,
不妨设x1>x2,作差得,ln ![]() =a(x1﹣x2),即a=
=a(x1﹣x2),即a= ![]() .
.
原不等式 ![]()
等价于 ![]()
令 ![]() ,则t>1,
,则t>1, ![]()
设 ![]() ,
, ![]() ,
,
∴函数g(t)在(1,+∞)上单调递增,
∴g(t)>g(1)=0,
即不等式 ![]() 成立,
成立,
故所证不等式 ![]() 成立.
成立.
【解析】(1)对f(x)求导,利用导数来判断f(x)的图形单调性;(2)(i)函数f(x)在其定义域内有两个不同的极值点转化为:方程lnx﹣ax=0在x>0上有两个不同根.(ii)x1 , x2分别是方程lnx﹣ax=0的两个根,即lnx1=ax1 , lnx2=ax2;不妨设x1>x2 , 作差得,ln ![]() =a(x1﹣x2),即a=
=a(x1﹣x2),即a= ![]() .原不等式
.原不等式 ![]() 等价于
等价于 ![]() .
.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.

【题目】如今,中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用![]() (单位:万元)和利润
(单位:万元)和利润![]() (单位:十万元)之间的关系,得到下列数据:
(单位:十万元)之间的关系,得到下列数据:
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
请回答:
(Ⅰ)请用相关系数![]() 说明
说明![]() 与
与![]() 之间是否存在线性相关关系(当
之间是否存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(Ⅱ)根据1的判断结果,建立![]() 与
与![]() 之间的回归方程,并预测当
之间的回归方程,并预测当![]() 时,对应的利润
时,对应的利润![]() 为多少(
为多少(![]() 精确到
精确到![]() ).
).
附参考公式:回归方程中![]() 中
中![]() 和
和![]() 最小二乘估计分别为
最小二乘估计分别为 ,
,![]() ,
,
相关系数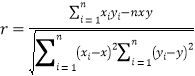 .
.
参考数据: ![]() .
.
