题目内容
【题目】如图,已知椭圆![]() 的离心率是
的离心率是![]() ,一个顶点是
,一个顶点是![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
,![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的任意两点,且
的任意两点,且![]() .试问:直线
.试问:直线![]() 是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
【答案】(Ⅰ)![]() (Ⅱ)直线
(Ⅱ)直线![]() 恒过定点
恒过定点![]()
【解析】
试题分析:(Ⅰ)设椭圆C的半焦距为c.求出b利用离心率求出a,即可求解椭圆C的方程;(Ⅱ)证法一:直线PQ的斜率存在,设其方程为y=kx+m.将直线PQ的方程代入![]() 消去y,设 P
消去y,设 P![]() ,Q
,Q![]() ,利用韦达定理,通过BP⊥BQ,化简求出
,利用韦达定理,通过BP⊥BQ,化简求出![]() ,求出m,即可得到直线PQ恒过的定点.证法二:直线BP,BQ的斜率均存在,设直线BP的方程为y=kx+1,将直线BP的方程代入
,求出m,即可得到直线PQ恒过的定点.证法二:直线BP,BQ的斜率均存在,设直线BP的方程为y=kx+1,将直线BP的方程代入![]() ,消去y,解得x,设 P
,消去y,解得x,设 P![]() ,转化求出P的坐标,求出Q坐标,求出直线PQ的方程利用直线系方程求出定点坐标
,转化求出P的坐标,求出Q坐标,求出直线PQ的方程利用直线系方程求出定点坐标
试题解析:(Ⅰ)解:设椭圆![]() 的半焦距为
的半焦距为![]() .依题意,得
.依题意,得![]() ,
,
且![]() ,
,
解得![]() .
.
所以,椭圆![]() 的方程是
的方程是![]() .
.
(Ⅱ)证法一:易知,直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]() .
.
将直线![]() 的方程代入
的方程代入![]() ,
,
消去![]() ,整理得
,整理得![]() .
.
设![]() ,
,![]() ,
,
则![]() ,
,![]() .(1)
.(1)
因为![]() ,且直线
,且直线![]() 的斜率均存在,
的斜率均存在,
所以![]() , 整理得
, 整理得![]() .(2)
.(2)
因为![]() ,
,![]() ,
,
所以![]() ,
,![]() .(3)
.(3)
将(3)代入(2),整理得
![]() .(4)
.(4)
将(1)代入(4),整理得![]() .
.
解得![]() ,或
,或![]() (舍去).
(舍去).
所以,直线![]() 恒过定点
恒过定点![]() .
.
证法二:直线![]() 的斜率均存在,设直线
的斜率均存在,设直线![]() 的方程为
的方程为![]() .
.
将直线![]() 的方程代入
的方程代入![]() ,消去
,消去![]() ,得
,得![]()
解得![]() ,或
,或![]() .
.
设![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() .
.
以![]() 替换点
替换点![]() 坐标中的
坐标中的![]() ,可得
,可得![]() .
.
从而,直线![]() 的方程是
的方程是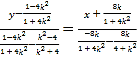 .
.
依题意,若直线![]() 过定点,则定点必定在
过定点,则定点必定在![]() 轴上.
轴上.
在上述方程中,令![]() ,解得
,解得![]() .
.
所以,直线![]() 恒过定点
恒过定点![]() .
.

练习册系列答案
相关题目