题目内容
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左焦点
)的左焦点![]() 与抛物线
与抛物线![]() 的焦点重合,直线
的焦点重合,直线![]() 与以原点
与以原点![]() 为圆心,以椭圆的离心率
为圆心,以椭圆的离心率![]() 为半径的圆相切.
为半径的圆相切.
(Ⅰ)求该椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线交椭圆于
的直线交椭圆于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
, ![]() 的垂直平分线与
的垂直平分线与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() ,
, ![]() 两点.记
两点.记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() .问:是否存在直线
.问:是否存在直线![]() ,使得
,使得![]() ,若存在,求直线
,若存在,求直线![]() 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)由已知得![]() ,
, 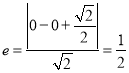 ,由此得椭圆方程;
,由此得椭圆方程;
(Ⅱ)假设存在直线AB,使得S1=S2,由题意直线AB不能与x,y轴垂直,设直线AB的方程为![]() (
(![]() )代入
)代入![]() 整理得
整理得![]() ,由此利用韦达定理、直线垂直、三角形相似等知识,结合已知条件能求出结果.
,由此利用韦达定理、直线垂直、三角形相似等知识,结合已知条件能求出结果.
试题解析:
(Ⅰ)由题意,得![]() ,
, 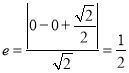 ,即
,即![]() ,∴
,∴![]() ,
, ![]()
∴所求椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)假设存在直线![]() 使
使![]() ,显然直线
,显然直线![]() 不能与
不能与![]() ,
, ![]() 轴垂直.
轴垂直.
∴直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]() (
(![]() ),
),
将其代入![]() 整理得
整理得![]() ,
,
设![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴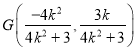 ,
,
∵![]() ,∴
,∴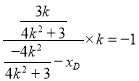 ,
,
解得![]() ,即
,即 ,
,
∵![]() ,∴
,∴![]() ,∴
,∴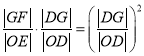 ,
,
即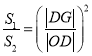 ,又∵
,又∵![]() ,∴
,∴![]() ,
,
∴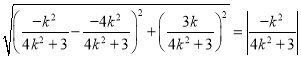 ,
,
整理得![]() 因为此方程无解,故不存在直线
因为此方程无解,故不存在直线![]() 满足
满足![]() .
.


练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
【题目】某学校高一 、高二 、高三三个年级共有 ![]() 名教师,为调查他们的备课时间情况,通过分层
名教师,为调查他们的备课时间情况,通过分层
抽样获得了![]() 名教师一周的备课时间 ,数据如下表(单位 :小时):
名教师一周的备课时间 ,数据如下表(单位 :小时):
高一年级 |
|
|
|
|
| |||
高二年级 |
|
|
|
|
|
|
| |
高三年级 |
|
|
|
|
|
|
|
|
(1)试估计该校高三年级的教师人数 ;
(2)从高一年级和高二年级抽出的教师中,各随机选取一人,高一年级选出的人记为甲 ,高二年级选出的人记为乙 ,求该周甲的备课时间不比乙的备课时间长的概率 ;
(3)再从高一、高二、高三三个年级中各随机抽取一名教师,他们该周的备课时间分别是![]() (单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为
(单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为![]() ,表格中的数据平均数记为
,表格中的数据平均数记为![]() ,试判断
,试判断![]() 与
与![]() 的大小. (结论不要求证明)
的大小. (结论不要求证明)