题目内容
某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果,结果有50个特等品.将这50个水果的质量数据分组,得到下边的频率分布表.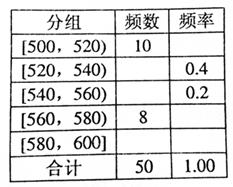
(1)估计该水果的质量不少于560g的概率;
(2)若在某批水果的检测中,发现有15个特等品,据此估计该批水果中没有达到特等品的个数.
(1)0.2;(2)285.
解析试题分析:本题主要考查频率分布表、频率的计算、分层抽样等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,在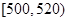 之间,利用“频率=频数÷样本总数”计算
之间,利用“频率=频数÷样本总数”计算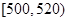 范围内的频率0.2,在
范围内的频率0.2,在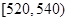 范围内的频数为20,在
范围内的频数为20,在 范围内的频数为10,在
范围内的频数为10,在 范围内的频率为0.16,在
范围内的频率为0.16,在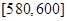 内的频率为0.04,频数为2,则第一问不少于560g的概率为
内的频率为0.04,频数为2,则第一问不少于560g的概率为 和
和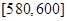 的频率之和;第二问,用分层抽样的方法列出表达式,解出未知数.
的频率之和;第二问,用分层抽样的方法列出表达式,解出未知数.
试题解析:(1)由已知可得该水果的质量不少于560g的概率
p=0.16+0.04=0.2. 6分
(2)设该批水果中没有达到特等品的个数为x,则有 ,解得x=285. 12分
,解得x=285. 12分
考点:频率分布表、频率的计算、分层抽样.

 阅读快车系列答案
阅读快车系列答案某中学一位高三班主任对本班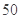 名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
| | 积极参加班级工作 | 不太主动参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太积极参加班级工作且学习积极性一般的学生的概率是多少?
(2)学生的积极性与对待班级工作的态度是否有关系?说明理由.
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
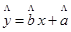
(2)试根据已求出的线性回归方程,预测记忆力为9的同学的判断力.
某公司生产产品A,产品质量按测试指标分为:指标大于或等于90为一等品,大于或等于 小于
小于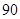 为二等品,小于
为二等品,小于 为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利
为三等品,生产一件一等品可盈利50元,生产一件二等品可盈利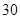 元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
元,生产一件三等品亏损10元.现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测,检测结果统计如下:
| 测试指标 | 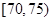 | 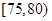 | 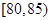 | 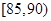 | 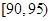 | 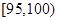 |
| 甲 | 3 | 7 | 20 | 40 | 20 | 10 |
| 乙 | 5 | 15 | 35 | 35 | 7 | 3 |
根据上表统计得到甲、乙两人生产产品A为一等品、二等品、三等品的频率分别估计为他们生产产品A为一等品、二等品、三等品的概率.
(1)计算甲生产一件产品A,给工厂带来盈利不小于30元的概率;
(2)若甲一天能生产20件产品A,乙一天能生产15件产品A,估计甲乙两人一天生产的35件产品A中三等品的件数.
在某种产品表面进行腐蚀性刻线实验,得到腐蚀深度y与腐蚀时间x之间相应的一组观察值,如下表:
| x/s | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 90 | 120 |
| y/μm | 6 | 10 | 10 | 13 | 16 | 17 | 19 | 23 | 25 | 29 | 46 |
某商场经营一批进价是30元/台的小商品,在市场试验中发现,此商品的销售单价x(x取整数)元与日销售量y台之间有如下关系:
| x | 35 | 40 | 45 | 50 |
| y | 56 | 41 | 28 | 11 |
(2)求日销售量y对销售单价x的线性回归方程;
(3)设经营此商品的日销售利润为P元,根据(1)写出P关于x的函数关系式,并预测当销售单价x为多少元时,才能获得最大日销售利润.
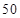 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为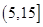 ,
,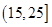 ,
,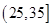 ,
, ,由此得到样本的重量频率分布直方图,如图
,由此得到样本的重量频率分布直方图,如图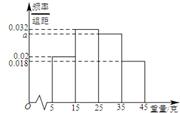
 的值;
的值; 组的频率为
组的频率为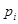 ,第
,第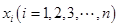 ,则样本数据的平均值为
,则样本数据的平均值为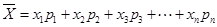 .)
.) 个小球,其中重量在
个小球,其中重量在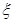 ,求
,求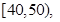
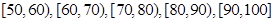 ,据此绘制了如图所示的频率分布直方图.
,据此绘制了如图所示的频率分布直方图. 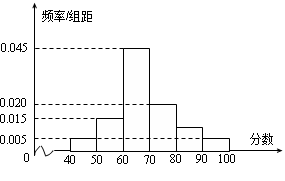
 的频率;
的频率; )
)