题目内容
假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
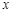 | 2 | 3 | 4 | 5 | 6 |
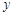 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
(1) ;(2)维修费约为12.38万元.
;(2)维修费约为12.38万元.
解析试题分析:(1)由于 知道y与x呈线性相关关系,就无需进行相关性检验;先由题中所给数据,求出 和
和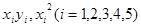 ,并求出它们的和
,并求出它们的和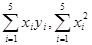 将这些值代入最小二乘法公式
将这些值代入最小二乘法公式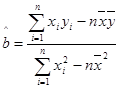 算得
算得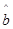 ,再由
,再由 求得
求得 ,从而求得回归直线方程;(2)由(1)取
,从而求得回归直线方程;(2)由(1)取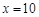 ,计算出对应的
,计算出对应的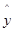 的值,即是估计使用年限为10年时,维修费的估计值,注意回答即可.
的值,即是估计使用年限为10年时,维修费的估计值,注意回答即可.
试题解析:(1)依题列表如下: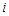
1 2 3 4 5 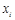
2 3 4 5 6 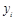
2.2 3.8 5.5 6.5 7.0 
4.4 11.4 22.0 32.5 42.0 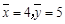

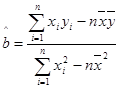
 ,
, 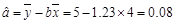 .
. 回归直线方程为
回归直线方程为 .
.
(2)当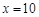 时,
时,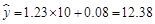 万元.
万元.
即估计用10年时,维修费约为12.38万元.
考点:线性回归.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | 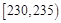 | 8 | 0.16 |
| 第二组 | 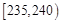 | ① | 0.24 |
| 第三组 | 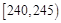 | 15 | ② |
| 第四组 | 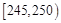 | 10 | 0.20 |
| 第五组 | 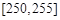 | 5 | 0.10 |
| 合 计 | 50 | 1.00 | |
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
“世界睡眠日”定在每年的3月21日,2009年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2000人参加调查,现将数据整理分组后如题中表格所示.
序号 | 分组睡眠时间 | 组中值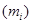 | 频数 (人数) | 频率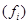 |
| 1 | 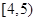 | 4.5 | 80 | ( ) |
| 2 | 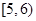 | 5.5 | 520 | 0.26 |
| 3 | 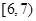 | 6.5 | 600 | 0.30 |
| 4 | 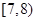 | 7.5 | ( ) | ( ) |
| 5 | 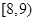 | 8.5 | 200 | 0.10 |
| 6 | 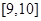 | 9.5 | 40 | 0.02 |
(1)求出表中空白处的数据,并将表格补充完整;
(2)画出频率分布直方图;
(3)为了对数据举行分析,采用了计算机辅助计算.分析中一部分计算见算法流程图,求输出的
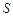 值。
值。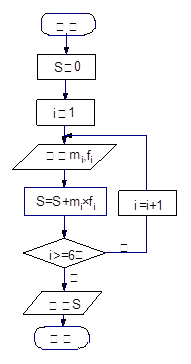
某公司销售A、B、C三款手机,每款手机都有经济型和豪华型两种型号,据统计12月份共销售1000部手机(具体销售情况见下表)
| | A款手机 | B款手机 | C款手机 |
| 经济型 | 200 | x | y |
| 豪华型 | 150 | 160 | z |
已知在销售1000部手机中,经济型B款手机销售的频率是0.21.
(1)现用分层抽样的方法在A、B、C三款手机中抽取50部,求应在C款手机中抽取多少部?
(2)若y
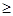 136,z
136,z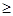 133,求C款手机中经济型比豪华型多的概率.
133,求C款手机中经济型比豪华型多的概率. 以下是某地搜集到的新房屋的销售价格 (万元)和房屋的面积
(万元)和房屋的面积 (
(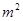 )的数据 ,若由资料可知
)的数据 ,若由资料可知 对
对 呈线性相关关系。
呈线性相关关系。
 | 80 | 90 | 100 | 110 | 120 |
| y | 48 | 52 | 63 | 72 | 80 |
试求:(1)线性回归方程;
(2)根据(1)的结果估计当房屋面积为
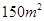 时的销售价格.
时的销售价格.参考公式:
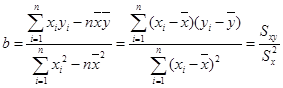
某中学一位高三班主任对本班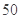 名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
名学生学习积极性和对待班级工作的态度进行长期的调查,得到的统计数据如下表所示:
| | 积极参加班级工作 | 不太主动参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太积极参加班级工作且学习积极性一般的学生的概率是多少?
(2)学生的积极性与对待班级工作的态度是否有关系?说明理由.



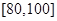 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在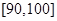 之间的概率;
之间的概率;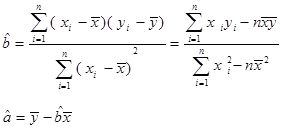
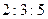 的
的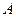 、
、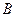 、
、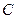 三所高校中,用分层抽样方法抽取
三所高校中,用分层抽样方法抽取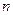 名志愿者,若在
名志愿者,若在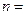 ▲ .
▲ .