题目内容
2.已知f(x)=$\left\{\begin{array}{l}{{2}^{x}(x≤2)}\\{f(x-2)(x>2)}\end{array}\right.$,则f(log27)=$\frac{7}{4}$.分析 由对数函数的性质判断出2<log27<3,根据函数解析式和指数的运算求出f(log27)的值.
解答 解:由题意知,f(x)=$\left\{\begin{array}{l}{{2}^{x}(x≤2)}\\{f(x-2)(x>2)}\end{array}\right.$,且2<log27<3,
所以f(log27)=f(log27-2)=${2}^{lo{g}_{2}^{7}-2}$=${2}^{lo{g}_{2}^{7}}•{2}^{-2}$=$\frac{7}{4}$,
故答案为:$\frac{7}{4}$.
点评 本题考查分段函数的函数值,对数函数的性质、指数的运算,注意自变量的范围,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.过点A(0,1)且与双曲线x2-y2=4仅有一个公共点的直线共有( )条.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 ,若当
,若当 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( ) B.
B.
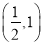 D.
D.
 如图,割线PBC经过圆心O,PB=OB=1,OB绕点O逆时针旋$\frac{2π}{3}$到OD,连PD交圆O于点E,则PE=$\frac{3\sqrt{7}}{7}$.
如图,割线PBC经过圆心O,PB=OB=1,OB绕点O逆时针旋$\frac{2π}{3}$到OD,连PD交圆O于点E,则PE=$\frac{3\sqrt{7}}{7}$. 如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=CD=2,M是线段AE上的动点.
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,AB=AD=DE=CD=2,M是线段AE上的动点.