题目内容
13. 如图,割线PBC经过圆心O,PB=OB=1,OB绕点O逆时针旋$\frac{2π}{3}$到OD,连PD交圆O于点E,则PE=$\frac{3\sqrt{7}}{7}$.
如图,割线PBC经过圆心O,PB=OB=1,OB绕点O逆时针旋$\frac{2π}{3}$到OD,连PD交圆O于点E,则PE=$\frac{3\sqrt{7}}{7}$.
分析 先由余弦定理求出PD,再根据割线定理即可求出PE,问题解决.
解答 解:由余弦定理得,PD2=OD2+OP2-2OD•OPcos120°=1+4-2×1×2×(-$\frac{1}{2}$)=7,
所以PD=$\sqrt{7}$.
根据割线定理PE•PD=PB•PC得,$\sqrt{7}$PE=1×3,
所以PE=$\frac{3\sqrt{7}}{7}$.
故答案为:$\frac{3\sqrt{7}}{7}$.
点评 已知三角形两边与夹角时,一定要想到余弦定理的运用,之后做题的思路也许会豁然开朗.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
1.某人射击一发子弹的命中率为0.8,现他射击19发子弹,理论和实践都表明,这19发子弹中命中目标的子弹数n的概率f(n)如下表,那么在他射击完19发子弹后,其中击中目标的子弹数最可能是( )
| n | 0 | 1 | … | k | … | 19 |
| F(n) | 0.219 | $C_{19}^1{(0.8)^1}{(0.2)^{18}}$ | … | $C_{19}^k{(0.8)^k}{(0.2)^{19-k}}$ | … | 0.819 |
| A. | 14发 | B. | 15发 | C. | 16发 | D. | 15或16发 |
3.2和-2的等比中项为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 不存在 |
 是直角三角形
是直角三角形 斜边
斜边 上一点,
上一点,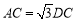 .
.
 ,求
,求 ;
; ,且
,且 ,求
,求 .
. 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1过点D(1,$\frac{3}{2}$),且右焦点为F(1,0)右顶点为A,过点F的弦为BC,直线BA,直线CA分别交直线l:x=m(m>2)于P、Q两点.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1过点D(1,$\frac{3}{2}$),且右焦点为F(1,0)右顶点为A,过点F的弦为BC,直线BA,直线CA分别交直线l:x=m(m>2)于P、Q两点.