题目内容
7.四棱锥P-ABCD的五个顶点都在半径为$\sqrt{3}$的半球面上,底面ABCD是边长为2的正方形,则顶点P到平面ABCD距离的最大值为$\sqrt{3}$-1.分析 求出球心到平面的距离,然后判断底面ABCD的中心与顶点P之间的距离即可.
解答 解:四棱锥-ABCD的底面是边长为2的正方形,点P,A,B,C,D均在半径为$\sqrt{3}$的同一半球面上,
则当顶点P到平面ABCD距离最大时,顶点P与底面ABCD的中心的连线经过球的中心,
四棱锥是正四棱锥,底面中心与顶点P之间的距离,
就是球的半径和球心与底面中心连线的长度之差.
球心到底面中心的距离为:$\sqrt{3-2}$=1.
所求距离为:$\sqrt{3}$-1.
故答案为:$\sqrt{3}$-1.
点评 本题考查球的内接体,几何体的高的求法,考查空间想象能力以及计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.若二项式(x+$\frac{a}{\root{3}{x}}$)8的展开式中x4的系数为7,则实数a=( )
| A. | 2$\root{3}{6}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{\root{3}{36}}{12}$ |
19.已知数列{an}的通项公式an=10n,n∈N+,bn=$\frac{1}{lg{a}_{2n-1}lg{a}_{2n+1}}$,则数列{bn}的前n项和Sn=$\frac{n}{2n+1}$.
16.下列选项中元素的全体可以组成集合的是( )
| A. | 蓝溪中学高二年个子高的学生 | B. | 蓝溪中学高职班的学生 | ||
| C. | 蓝溪中学高二年学习好的学生 | D. | 校园中茂盛的树木 |
17.已知f(x)=x+x3,且x1+x2<0,x2+x3<0,x3+x1<0则( )
| A. | f(x1)+f(x2)+f(x3)>0 | B. | f(x1)+f(x2)+f(x3)<0 | ||
| C. | f(x1)+f(x2)+f(x3)=0 | D. | f(x1)+f(x2)+f(x3)符号不能确定 |
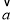 与
与 的夹角等于
的夹角等于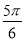 ,如果
,如果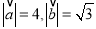 ,那么
,那么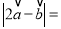 ( )
( )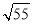 B.9 C.
B.9 C.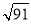 D.10
D.10