题目内容
14.若(1-2x)5=a0+a1x+a2x2+…+a5x5,那么|a0|+|a1|+|a2|+…+|a5|=243,a1+a3+a5=-122.分析 根据|a0|+|a1|+|a2|+…+|a5|是(1+2x)5的展开式中各项系数的和,令x=1求出它的值;
再由x=1求出a0+a1+a2+…+a5的值,x=-1求出a0-a1+a2-…-a5的值,作差即可求出a1+a3+a5的值.
解答 解:∵(1-2x)5=a0+a1x+a2x2+…+a5x5,
∴|a0|+|a1|+|a2|+…+|a5|是(1+2x)5的展开式中各项系数的和,
令x=1,得(1+2x)5的展开式中各项系数和为
|a0|+|a1|+|a2|+…+|a5|=(1+2)5=35=243;
又x=1时,(1-2)5=a0+a1+a2+…+a5=-1,
x=-1时,(1+2)5=a0-a1+a2-…-a5=243,
两式相减,得2a1+2a3+2a5=-1-243=-244,
∴a1+a3+a5=-122.
故答案为:243、-122.
点评 本题考查了二项式定理的应用问题,解题的关键是利用特殊值进行计算,是基础题目.

练习册系列答案
相关题目
19.已知数列{an}的通项公式an=10n,n∈N+,bn=$\frac{1}{lg{a}_{2n-1}lg{a}_{2n+1}}$,则数列{bn}的前n项和Sn=$\frac{n}{2n+1}$.
3.2和-2的等比中项为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 不存在 |
 是直角三角形
是直角三角形 斜边
斜边 上一点,
上一点,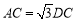 .
.
 ,求
,求 ;
; ,且
,且 ,求
,求 .
. 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1过点D(1,$\frac{3}{2}$),且右焦点为F(1,0)右顶点为A,过点F的弦为BC,直线BA,直线CA分别交直线l:x=m(m>2)于P、Q两点.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1过点D(1,$\frac{3}{2}$),且右焦点为F(1,0)右顶点为A,过点F的弦为BC,直线BA,直线CA分别交直线l:x=m(m>2)于P、Q两点. 如图所示,在四棱锥P-ABCD中,PA⊥底面 ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点,证明:
如图所示,在四棱锥P-ABCD中,PA⊥底面 ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点,证明: