题目内容
设a1,a2,…,a50是从-1,0,1这三个整数中取值的数列,若a1+a2+…+a50=9,
且(a1+1)2+(a2+1)2+…+(a50+1)2=107,则a1,a2,…,a50中有0的个数为( )
且(a1+1)2+(a2+1)2+…+(a50+1)2=107,则a1,a2,…,a50中有0的个数为( )
| A.10 | B.11 | C.12 | D.13 |
B
将已知的等式展开整理得a12+a22+a32+…+a502=39,故此50个数中有11个数为0.
故选B.
故选B.

练习册系列答案
相关题目
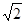 ,
,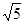 ,
,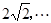 ,则
,则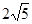 是这个数列的第( )项
是这个数列的第( )项 ,如果数列
,如果数列 满足:
满足: 的任意一个排列都可以在原数列中删去若干项后按数列原来顺序排列而得到,则称
的任意一个排列都可以在原数列中删去若干项后按数列原来顺序排列而得到,则称 由;
由; ,
, …,求{cn}的通项公式.
…,求{cn}的通项公式. 的通项公式
的通项公式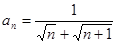 ,则该数列的前( )项之和等于9。
,则该数列的前( )项之和等于9。 中,
中, 且点P
且点P 在直线
在直线 上.
上. 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前 项和
项和 .
. 中,
中,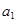 =1,
=1,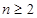 时,
时,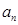 =2
=2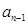 +1,则
+1,则 项之和
项之和 等于( )
等于( )

