题目内容
(几何证明选讲选做题)如图,PC、DA为⊙O的切线,A、C为切点,AB为⊙O的直径,若DA=2,CD:DP=1:2,则AB=______.


∵DA、DC均为过圆外一点D的切线
∴DA=DC=2
又∵CD:DP=1:2,
∴DP=4,故有CP=6
在直角三角形DAP中,PA=
=2
由线割线定理得PC2=PA•PB
解得PB=6
则AB=PB-PA=4
故答案为:4
∴DA=DC=2
又∵CD:DP=1:2,
∴DP=4,故有CP=6
在直角三角形DAP中,PA=
| DP2-DA2 |
| 3 |
由线割线定理得PC2=PA•PB
解得PB=6
| 3 |
则AB=PB-PA=4
| 3 |
故答案为:4
| 3 |

练习册系列答案
相关题目
 ,
,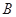 ,
, 三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从
三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从






 ,即每16人抽取一个人.在1~16中随机抽取一个数,如果抽到的是7,则从33~48这16个数中应取的数是( )
,即每16人抽取一个人.在1~16中随机抽取一个数,如果抽到的是7,则从33~48这16个数中应取的数是( ) 服从正态分布
服从正态分布 ,若
,若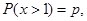 则
则 .
. 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,A为弧CE的重点,DE交AB于点F,且AB=2BP=4,求PF的长度。
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,A为弧CE的重点,DE交AB于点F,且AB=2BP=4,求PF的长度。