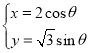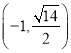题目内容
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),与圆
为参数),与圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)设直线![]() 与
与![]() 轴和
轴和![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() ,
,![]() 为圆
为圆![]() 上的任意一点,求
上的任意一点,求![]() 的最大值.
的最大值.
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,求
两点,求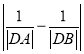 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用直线方程求得线段![]() ,再求得点
,再求得点![]() 到直线
到直线![]() 的最大距离,计算出面积即可;
的最大距离,计算出面积即可;
(2)写出直线![]() 的参数方程,代入圆
的参数方程,代入圆![]() 化简,利用几何意义即可得到结论.
化简,利用几何意义即可得到结论.
(1)圆![]() 圆心坐标为
圆心坐标为![]() ,半径为2,设圆
,半径为2,设圆![]() 圆心坐标为
圆心坐标为![]() ,半径为2,
,半径为2,
由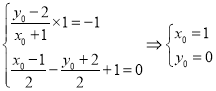 ,所以圆
,所以圆![]() 的方程为
的方程为![]() .
.
因为直线![]() 的极坐标方程是
的极坐标方程是![]() ,即
,即![]() ,由
,由![]() ,得直线
,得直线![]() 的直角坐标方程为
的直角坐标方程为![]() .点
.点![]() 到直线
到直线![]() 的最大距离
的最大距离 ,由
,由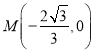 ,
,![]() 知
知![]() 的最大值为
的最大值为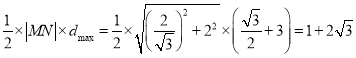 .
.
即![]() 的最大值为
的最大值为![]() .
.
(2)因为直线![]() 的倾斜角为
的倾斜角为![]() ,所以直线
,所以直线![]() 的参数方程为
的参数方程为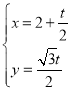 (
(![]() 为参数),①
为参数),①
圆![]() 的方程为
的方程为![]() ,②联立①②得
,②联立①②得![]() .
.
设![]() ,
,![]() 两点对应的参数分别为
两点对应的参数分别为![]() ,
,![]() 则
则![]() ,
,![]() ,
,
故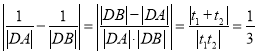 .
.

 津桥教育计算小状元系列答案
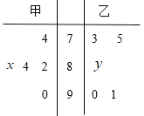
津桥教育计算小状元系列答案【题目】为了提高生产线的运行效率,工厂对生产线的设备进行了技术改造.为了对比技术改造后的效果,采集了生产线的技术改造前后各![]() 次连续正常运行的时间长度(单位:天)数据,并绘制了如茎叶图:
次连续正常运行的时间长度(单位:天)数据,并绘制了如茎叶图:
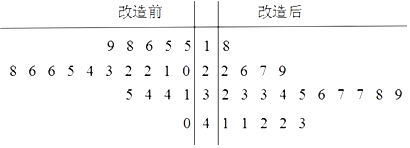
(1)①设所采集的![]() 个连续正常运行时间的中位数
个连续正常运行时间的中位数![]() ,并将连续正常运行时间超过
,并将连续正常运行时间超过![]() 和不超过
和不超过![]() 的次数填入下面的列联表:
的次数填入下面的列联表:
超过 | 不超过 | |
改造前 |
|
|
改造后 |
|
|
②根据①中的列联表,能否有![]() 的把握认为生产线技术改造前后的连续正常运行时间有差异?
的把握认为生产线技术改造前后的连续正常运行时间有差异?
附: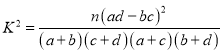 .
.
|
|
|
|
|
|
|
|
(2)工厂的生产线的运行需要进行维护,工厂对生产线的生产维护费用包括正常维护费、保障维护费两种.对生产线设定维护周期为![]() 天(即从开工运行到第
天(即从开工运行到第![]() 天
天![]() 进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为
进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为![]() 万元/次;保障维护费第一次为
万元/次;保障维护费第一次为![]() 万元/周期,此后每增加一次则保障维护费增加
万元/周期,此后每增加一次则保障维护费增加![]() 万元.现制定生产线一个生产周期(以
万元.现制定生产线一个生产周期(以![]() 天计)内的维护方案:
天计)内的维护方案:![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() .以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.