题目内容
【题目】已知f(x)＝|2x－1|－|x＋1|.
(1)将f(x)的解析式写成分段函数的形式，并作出其图象；
(2)若a＋b＝1，对a，b∈(0，＋∞)，
＋
≥3f(x)恒成立，求x的取值范围．
【答案】（1）见解析（2）[－1,5]
【解析】试题分析：（1）讨论x的范围：x＜﹣1，﹣1≤x≤
，x＞，去绝对值，可得f（x）的分段函数的解析式，由分段函数图象画法可得其图象；
（2）运用乘1法和基本不等式，可得
+
的最小值，由题意可得|2x﹣1|﹣|x+1|≤3，结合图象即可得到所求x的范围．
试题解析：
(1)由已知，得f(x)＝
函数f(x)的图象如图所示．
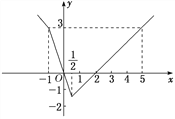
(2)∵a，b∈(0，＋∞)，且a＋b＝1，
∴
＋
＝
(a＋b)＝5＋
≥5＋2
＝9，当且仅当
＝
，即a＝
，b＝
时等号成立．
∵＋≥3(|2x－1|－|x＋1|)恒成立，
∴|2x－1|－|x＋1|≤3，
结合图象知－1≤x≤5，
∴x的取值范围是[－1,5]．
练习册系列答案
阅读快车系列答案
相关题目
