题目内容
已知椭圆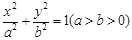 的右焦点为
的右焦点为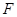 ,
, 点在椭圆上,以
点在椭圆上,以 点为圆心的圆与
点为圆心的圆与 轴相切,且同时与
轴相切,且同时与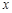 轴相切于椭圆的右焦点
轴相切于椭圆的右焦点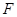 ,则椭圆
,则椭圆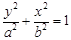 的离心率为 .
的离心率为 .
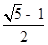
解析试题分析:根据题意可知,椭圆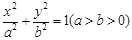 的右焦点为
的右焦点为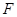 ,
, 点在椭圆上,由于以
点在椭圆上,由于以 点为圆心的圆与
点为圆心的圆与 轴相切,可知圆心的横坐标即为圆的半径,且同时与
轴相切,可知圆心的横坐标即为圆的半径,且同时与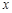 轴相切于椭圆的右焦点
轴相切于椭圆的右焦点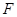 ,则说明了PF垂直于x轴,且利用椭圆的通径长为
,则说明了PF垂直于x轴,且利用椭圆的通径长为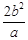 则说明半径r=
则说明半径r=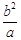 ,那么点P的横坐标为C,故可知
,那么点P的横坐标为C,故可知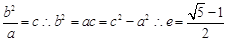 ,因此答案为
,因此答案为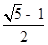
考点:本试题考查了椭圆的性质运用。
点评:解决该试题的关键是能结合题目中圆于两坐标轴相切,则说明了点P的坐标,然后利用半径一样来得到a,b,c的关系式,进而求解s椭圆的离心率,属于中档题。

练习册系列答案
相关题目
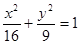 的焦距是 ,焦点坐标为
的焦距是 ,焦点坐标为 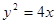 的焦点为F,过抛物线在第一象限部分上一点P的切线为
的焦点为F,过抛物线在第一象限部分上一点P的切线为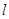 ,过P点作平行于
,过P点作平行于 轴的直线
轴的直线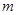 ,过焦点F作平行于
,过焦点F作平行于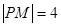 ,则点P的坐标为 。
,则点P的坐标为 。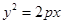 的焦点与双曲线
的焦点与双曲线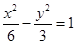 的右焦点重合,则
的右焦点重合,则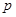 的值 .
的值 .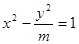 的一个焦点F作它的一条渐近线的垂线FM,垂足为M并且交
的一个焦点F作它的一条渐近线的垂线FM,垂足为M并且交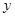 轴于E,若M为EF中点,则
轴于E,若M为EF中点,则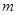 =___________.
=___________.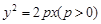 的焦点在圆
的焦点在圆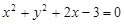 上,则
上,则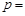 .
.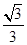 ,且与双曲线
,且与双曲线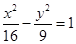 有相同的焦距,则椭圆的标准方程为________________________.
有相同的焦距,则椭圆的标准方程为________________________. 中,
中,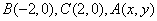 ,给出
,给出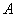 的轨迹方程,下表给出了一些条件及方程:
的轨迹方程,下表给出了一些条件及方程: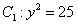
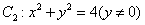
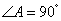
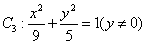
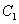 、
、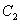 、
、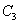 填入)
填入)  的左、右焦点,点P是双曲线上的点,且|P F1|=3,则|PF2|的值为 .
的左、右焦点,点P是双曲线上的点,且|P F1|=3,则|PF2|的值为 .